二进制及其它进制
通过前面对所谓的"球信息系统"的介绍, 其实已经摸到了二进制的边.
由来
在下述的表达中:
绿绿=阴天
绿红=刮风
红绿=下雨
红红=晴天
令: 0=绿; 1=红, 替换一下, 就得到了:
00=阴天
01=刮风
10=下雨
11=晴天
这样一种表示, 其实就是所谓的二进制了.
二进制的位数
如果扩展到三位, 同样的替换操作, 结果就是这样:
000=阴天
001=冰雹
010=刮风
011=沙尘暴
100=台风
101=下雨
110=下雪
111=晴天
可见二进制并没有什么神秘之处, 十进制有 0-9 十个数字 一个位上可以用这任意十个数字中的一个, 因此一位就足以表达十种情况, 两个位就可以表达 10 × 10 = 100 种情况, 三个位就可以表达 1000 种.
而二进制一个位只有 0 和 1 两个数字, 但一个位上的不足可以用多个位来弥补. 比如, 用两个位就可以表达 2 × 2 = 4 种情况, 三个位就是 8 种, 以此类推, 要表达 1000 种情况, 至少需要 10 个位.
就好比前者有十种颜色不同的球, 因此只用少数几个位就可以排列出很多不同状态; 后者只有两种颜色的球, 但它一样可以排列出很多不同状态, 只是更费球而已.
注: 210=1024, 比 1000 略多. 在要求不那么严格的情况下, 可以近似认为 210=103.
同理 220≈1000 × 1000, 也即是一百万. 230 则是十亿级别.
在表示诸如文件大小方面, 这三个级别也即所谓的 KB(千字节级别), MB(百万字节级别), GB(十亿字节级别).
因此完全可以用二进制的数去表示十进制的那些整数, 比如(左边为二进制, 右边为十进制):
00=0
01=1
10=2
11=3
在这里, 二进制的 10 表示的不是十, 而是二; 同理, 11 不是十一, 而是三.
两位二进制可以表达四种状态, 三位就可以表达八种:
000=0
001=1
010=2
011=3
100=4
101=5
110=6
111=7
最多表示到 7, 要表示 0-9 十种符号, 二进制需要拓展到四位:
0000=0
0001=1
0010=2
0011=3
0100=4
0101=5
0110=6
0111=7
1000=8
1001=9
四位二进制总共可以表达 16 种状态, 可以表示 0~15 这 16 个不同的数字, 因此只表示 10 个数字还有些剩余, 这里没有列出所有的情况.
目前来看, 你可能还不是很熟悉以及习惯二进制, 你更熟悉的是十进制, 甚至说看到 1000, 你首先想到的是十进制的 一千, 而不是二进制的 八. 我们之所以青睐二进制, 是因为在电路中更容易表示. 既然进制间是等价的, 你是否思考过这样的问题, 为何我们人类青睐十进制呢?
为什么是十进制?
人类在大约 7 万年前走出非洲, 分散到各地形成了各种文明, 往往在独自演化, 但为何单单在计数这一问题上, 常常不约而同选用了十进制呢? 没错, 答案就在我们的双手上, 我们的十根指头与我们的十进制之间绝不是巧合.
设想一下原始人类的一次狩猎大丰收, 一个首领兴奋地用指头在数着他们捕获的羊, 一只, 两只...哇, 全部手指用光了还没数完, 只好先在地上标识一下先, 然后再把指头全部收回继续清点.
那么, 这么一个标识的动作就是 进位 的雏形了, 而我们最终形成对十进制的偏好也就不足为奇了.
其它的可能
据说非洲有部落是采用 20 进制, 有学者去考察, 发现他们数数时把脚指头也用上了, 难怪呢! 而人其实有时会患上一种称为多指畸形的遗传性疾病, 其中以六指症最为多见:
其实说是畸形是因为他们是少数派, 如果他们成为主流, 我们可能就会习惯使用十二进制了!
而怕老鼠的喵星人--哆啦 A 梦则可能喜欢二进制:

难道二进制真的是未来的趋势? 据作者设定, 它的生日是 2112 年 9 月 3 日. 掐指头一算, 哎呀, 还不到 100 年了! 话说小时候看书时觉得 22 世纪是件很遥远的事~
不过跟别人猜拳时就悲剧了:

而龙虾们如果有一天也能建立自己的文明, 那么它们就可能是用四进制了:
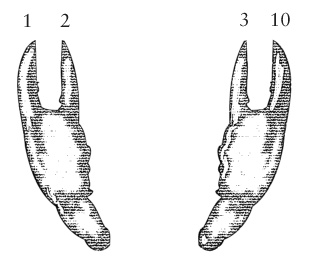
图片来自《编码:隐匿在计算机软硬件背后的语言》(Code: The Hidden Language of Computer Hardware and Software)一书.
广义的进制
如果我们把标准放松一点, 就不难发现人类社会中是存在很多的进制的.
比如以时间为例, 它混合了各种的进制. 小时是 12 或者 24 进制, 而分秒则是 60 进制. 只不过我们还是用十进制方式来书写它们. 23:59:59, 再加一秒是 00:00:00, 因为满 60 或者满 24 就要进位了, 进位后就归零了.
如果注意到 12 可以被 2, 3, 4, 6 整除, 而 60 则能被 2, 3, 4, 5, 6 整除. 那么采用这样的进制是有助于去更细地划分它们的.
而货币方面, 比如英国曾经是这样的:1 英镑等于 20 先令, 而 1 先令又等于 12 便士.
1 先令等于 12 便士自然也能使得它易于分割.
而我们中国古代的秤, 斤两之间曾经采用过 16 进制.
你以为“半斤八两”是怎么来的?
16 进制自然可以使得对一斤多次取半还能取整.
进制的总结
下面对各种进制做些小结.
N 进制有 N 个不同的数字(符号).
所以, 十进制就有十个不同数字: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9;
那么, 二进制就有两个不同数字: 0, 1; (借用了十进制的符号)
而八进制就有八个不同数字: 0, 1, 2, 3, 4, 5, 6, 7; (此处同样借用了十进制的符号)
而计算机世界里另一个经常使用的进制是十六进制. 对于十六进制而言, 即便借了十进制的全部符号还是不够用, 此时要么发明一些新的符号, 要么就再借用一些别的符号了.
对于十六进制, 实际借用了 6 个大写字母, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
N 进制逢 N 进 1.
十进制逢十进一, 二进制就是逢二进一.
对于二进制, 1+1 就要进位了, 因为结果是 2, 但二进制根本不存在 2 这个符号, 最大也就是 1. 进位后加位归零, 结果是 10(二进制).

反复加一, 可以得到更多的值, 小 1 表示有进位:
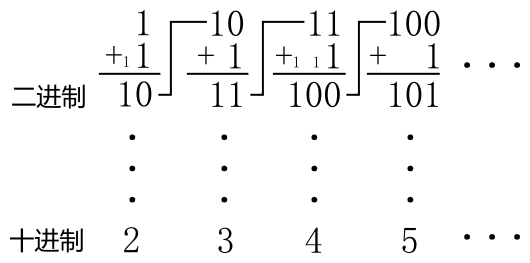
以下为十进制与二进制及十六进制的一个对应表:
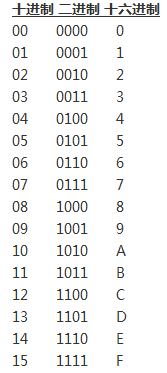
N 进制一个位最多只能表示 N 种不同状态, 要想表示更多的状态, 就要用更多的位. 两个位能最多表示 N×N 种状态, 三个位能表示 N×N×N 种状态, 依次类推.
一位 16 进制能表示 16 种状态, 两位则能表示 16×16=256 种状态.
一位十进制能表示 10 种状态, 两位则能表示 10×10=100 种状态.
同理, 一位二进制能表示 2 种状态, 两位则能表示 2×2=4 种状态.
自然, 要表示同样多种状态, 二进制比十进制需要更多的位数. 正如上面显示, 至少 4 位才能表示.
但尽管如此, 任何一个十进制整数都是可以用二进制来表示的. 用康托尔的话来说就是两个无穷集合是一一对应的.
二进制的优势
以一位数字的加法表为例, 如果使用的是十进制, 严格地讲, 有 10×10=100 种规则需要考虑.
想想我们曾经背过的九九乘法表, 它已经去掉了 0, 以及结合了交换律去掉了一些重复的情况, 却还依然有高达 45 个条目, 作为加法表, 也是如此.
虽然我们没有背过一位数加法表, 但经过反复练习, 实际上我们已经把它背下来了. 任何两个一位数的加法的和, 我相信几乎所有受过小学教育的人都能脱口而出. 就如同背过九九乘法表的人能对任何两个一位数的乘法的积也能脱口而出那样.
另: 多位的加法, 则采用拆分为多个一位的加法, 然后反复运用一位加法表里的规则.
如果采用二进制呢? 这个数目就大大减少了.
对于 N 进制而言, 有 N×N 种规则需要考虑. 因此, 对二进制而言, 只有四条规则.
二进制的加法表只有以下四条规则:
0+0=00,
0+1=01,
1+0=01,
1+1=10.
以上, 和采用两位来表示, 因为最后一条规则会产生进位, 一位不足以表达. 为规整起见, 前三条也就全部采用两位了.
乘法表甚至更简单, 因为不涉及进位, 积只需一位即可:
0×0=0,
0×1=0,
1×0=0,
1×1=1.
如果不考虑与 0 相乘的情况, 则只有一个条目: 1×1=1.
对比一下二进制的 一一乘法表 与十进制的 九九乘法表:
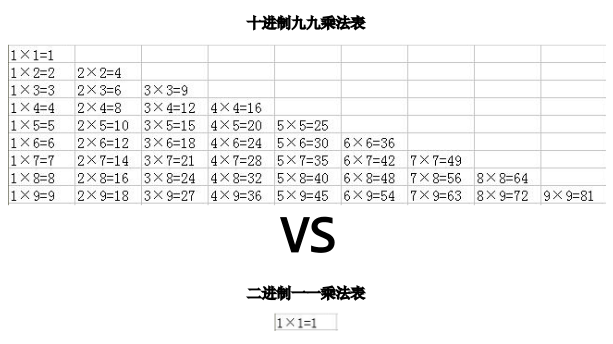
啊, 如果从一开始就采用二进制该多好, 这画面想想也要醉了, 再笨的熊孩子估计也能分分钟就掌握它们!
二进制的代言人, "蔡10"小姐就在一首歌里感慨地唱道: "那画面太美我不敢看..."(《布拉格广场》, 蔡依林 & 周杰伦)
我们现在觉得用二进制不方便, 看着不习惯, 那大概是因为没有从小就接受这样的方式.
如果你天天接触, 估计你也会习惯了. 有这么一种说法:
世界有 10 种人, 一种是懂二进制的, 一种是不懂的.

国家需要你这种懂二进制的!
关于进制的问题, 就说到这里. 有了以上基础, 在下一篇将介绍如何构建最终的二进制简易加法器.