前三条加法规则的实现

前面说到, 最简单的加法包含下述四条规则:

0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 2

现在已经能够表示及显示 0 和 1 了, 这已经足以让我们实现前三条加法规则了:

0 + 0 = 0
0 + 1 = 1
1 + 0 = 1

现在一条一条来分析.

0 + 0 的情况

首先是 0 + 0, 显然, 哪怕你什么都不做, 这个电路看上去就已经"实现"了 0 + 0 = 0:

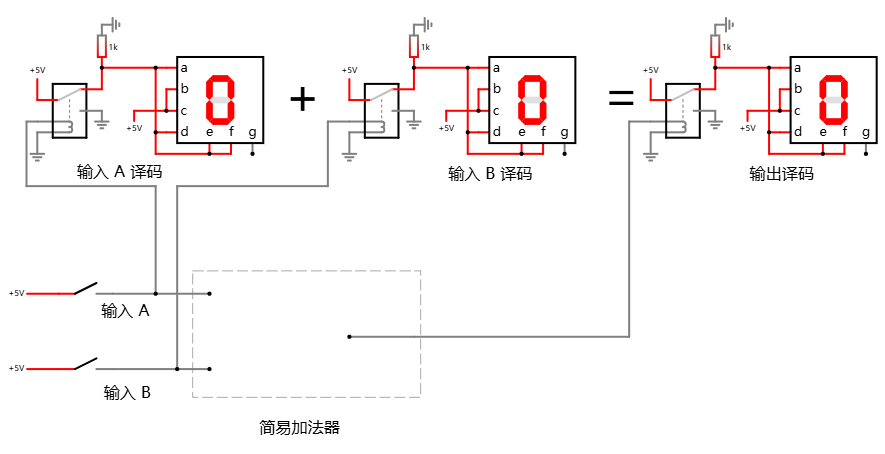
至少在显示层面看上去确实如此:

那么再来看 0 + 1 的情况, 那么也很简单, 拉一条导线把输入端 B 和输出端接起来即可.

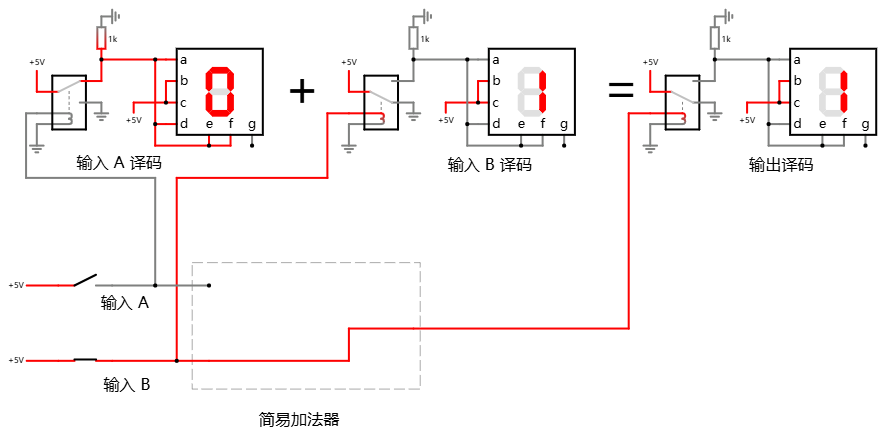
当然, 你还得兼容 0 + 0 = 0 的情况, 不能说"按下葫芦浮起瓢", 这个电路是需要同时实现所有的三条规则的.

实现了新的规则却破坏了旧规则是不行的, "只听新人笑, 哪闻旧人哭"是不好的, 我们不能喜新厌旧.

不过比较幸运的是, 旧的规则没有被破坏:

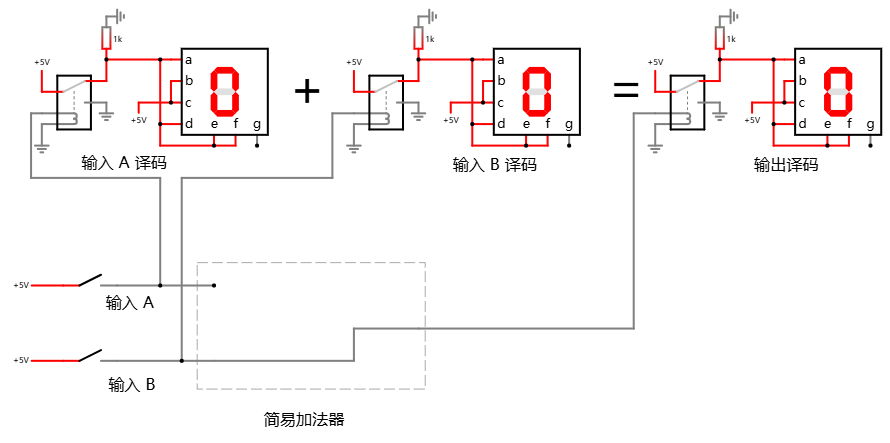
可以看到, 0 + 1 = 1, 而 0 + 0 = 0 也依然成立.

现在只剩一种情况了, 自然, 很容易想到, 把输入端 A 也连接到输出端, 似乎就解决了问题, 但实际操作起来, 会发现显示层面出了点状况:

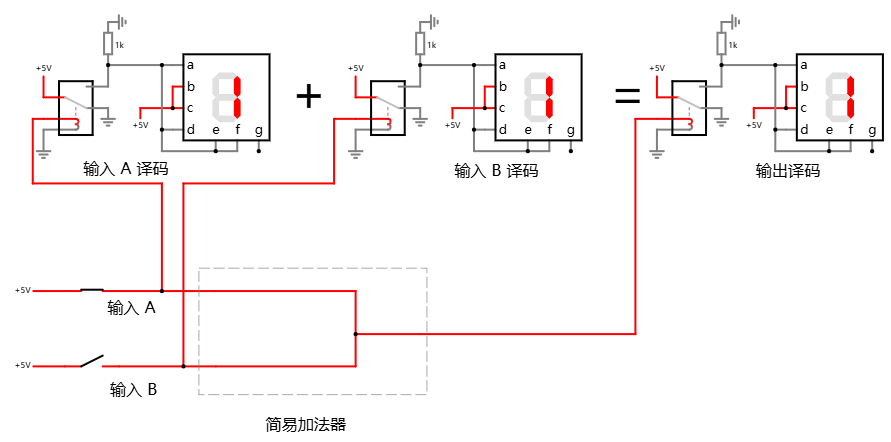
尽管 B 端没有闭合, 但因为内部彼此连接, 电流从 A 端"倒灌"回来 B 端, 因此, 尽管从开关的输入情况来看, 做的是 1 + 0, 但显示却成了 1 + 1.

另: 如果两个开关都闭合, 还会导致模拟器异常. 可能与模拟器内部具体实现的一些缺陷有关.

关于 circuitjs 异常及其处理, 参考模拟器异常处理

当然, 你可能会争辩说, 不考虑显示的情况就是 OK 了, 而且可以验证它也满足其它两种情况:

在 0 + 1 的情况下同样需要忽略显示的情况, 只有 0 + 0 的情况下显示才是 OK 的.

那么怎么解决这个倒灌的问题. 有两种思路, 一种是引入 二极管 这种具有 单向导电性 的器件.

实际上, 前面一直用的 LED 也有这样的性质, 前面也提到过, 如果接反了它就不会亮.

事实上, LED 的英文就是 Light-emitting Diode, 也就是所谓的"发光二极管".

另一种方案则要改变思路, 利用继电器的间接控制功能达到目的.

两种方案你都可以先自己想想怎么去实现, 或许你还可能想出第三种方案! 我们并没有标准答案! 达到目的的方案都是可以考虑的.