四位加法器
一个四位加法器的原型如下:
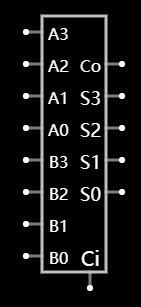
相对于两位的加法器, 两个输入和输出都扩展为了 4 位:
- 两个四位的输入
A3,A2,A1,A0和B3,B2,B1,B0; - 一个进位输入
Cin(Carry in); - 一个两位的输出
S3,S2,S1,S0; - 一个进位的输出,
C(Carry out).注: 这里直接用的就是系统自带的4位加法器的原型.
直接由全加器去构建
四位加法器的构建有几种方式. 一种还是直接从四个全加器开始构建:
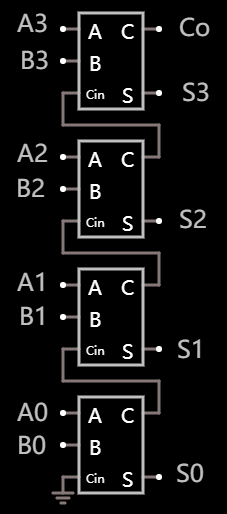
四位加法器, 四个全加器 在线可互动操作示例
具体 创建子电路 过程此处从略, 读者可以自行实验.
另: 此处使用的二极管是为了规避模拟器实现上的缺陷. 下同.
通过两位加法器去构建
除了直接使用多个全加器的方式, 考虑到先前已经有了两位加法器, 也可以以它为基础去构建, 其效果如下:
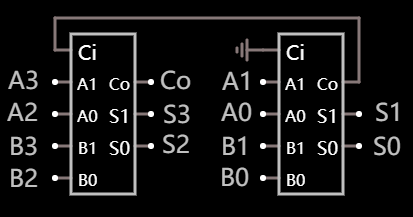
左边的模块处理高两位, 右边的模块处理低两位. 可以说, 相对而言更加简单了些. 归根结底, 都是用了全加器.
最后, 仍旧是利用前面说到的 创建子电路 的方式标识出各个节点名称
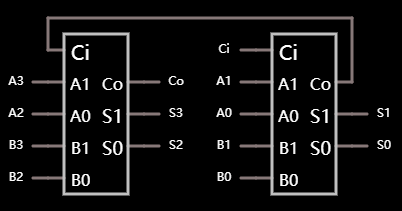
四位加法器, 输入与输出标识 在线可互动操作示例
然后创建子电路, 最后添加子电路实例:

也即是最开头处看到的原型.
配合上显示等模块, 可以说, 现在 LED 数码管的能力终于可以得到充分的发挥了. 现在的电路也不再是只能做 1 + 1 = 2 之类的了.
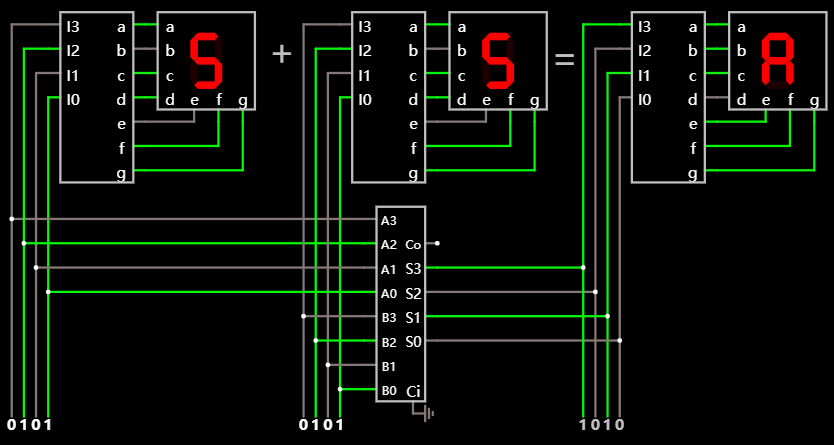
下图演示了 4 + 5 的情形:
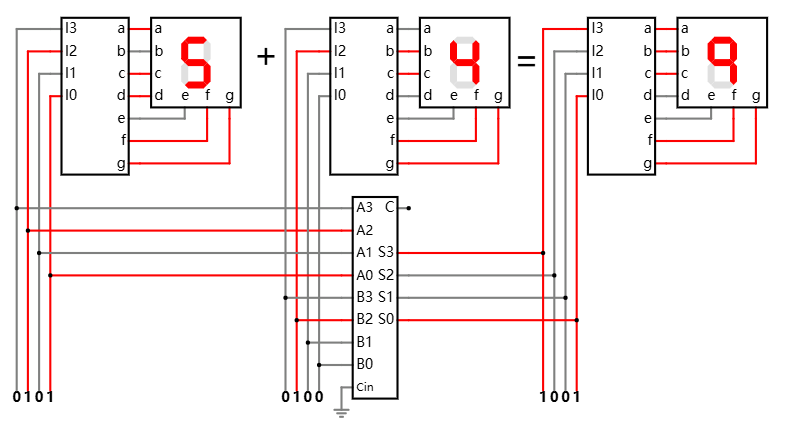
四位加法器, 计算演示 4 + 5 在线可互动操作示例
事实上, 扩展到了多位加数后, 又不得不面对新的显示问题.
比如, 假如执行 5 + 5, 那么结果是 10, 输出展示处首先就需要两个 LED 了.
此外, 还面临着如何把二进制的输出切割成两段十进制输出的问题等.
注: 目前的 LED 译码显示支持 16 进制, 对于 5 + 5, 它会显示一个类似 A 字母的图案, 因为在 16 进制中, A 代表 10.
而且, 如果我们愿意的话, 还可以继续拓展为 8 位, 乃至 16 位, 如此一来, 能加的数就很大了.
输入的问题
不过, 尽管能加比较大的数了, 但当位数拓展之后的面临的另一个问题是输入的便利性.
现在依然是使用 逻辑输入 开关以二进制的方式给出要加的两个数. 如果我们把这个多位加法器提供给用户, 说它能帮助你做加法, 但你首先得把要加的两个十进制数转换为二进制数.
那么用户可能就不乐意使用了, 而且他们不一定知道怎么转换这个进制. 必须给用户一个便利的方式指定要加的数, 在下一章节, 我们再来具体讨论这个问题及其解决方案.