利用继电器的间接控制
前面说到了二极管的方案, 这种方案虽然解决了前述的问题, 但它的一个很明显的弊端就是输出是从输入直接过来的, 这种方式局限性很大.
比如, 前面就碰到的一个类似问题, 输出低电平时想让 LED 数码管显示一个 0, 只能依赖继电器去间接控制.
现在, 观察一下三组规则, 总结起来无非就是要表达这样一个意思:
有一个开关闭合时, 输出高电平(灯亮).
当有多个开关时, 只要闭合其中一个, 就能让灯点亮, 这会让你想起什么电路呢? 显然, 并联电路就具有这样的性质:

并联电路的四种情况 在线可互动操作示例
注意: 现实世界中, 最后一种情况不需要添加电阻, 像下面这样就行了:
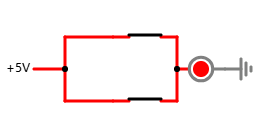
但这样的电路在模拟器中会有问题, 会报所谓的 "无电阻电压源/导线回路" 的异常, 并导致模拟器停止运行.
因为开关和导线在模拟器中均被认为是零电阻的, 当两个开关都闭合时, 模拟器认为局部形成了一个零电阻的回路, 当然, 这么连电路是没有问题的, 这个只能算是模拟器实现上的的一个缺陷.
加一个电阻就是为了规避这样的问题. 事实上, 随便在空白处把三根导线连成一个闭合三角形均会导致类似的问题.
关于 circuitjs 异常及其处理, 参考 模拟器异常处理
其实前面的二极管方案就是并联的, 只是开关都在外面, 现在只需把控制开关移到内部, 也即是让继电器作为开关, 然后外部的开关再控制继电器里面的开关:
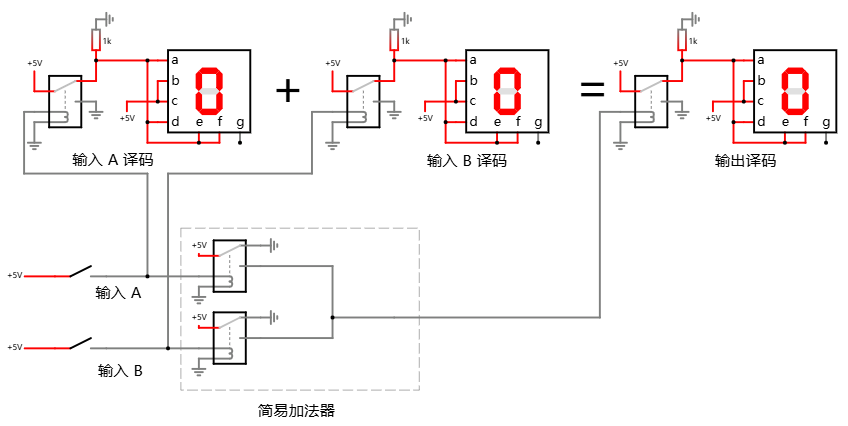
上面是 0 + 0 的情况, 然后 0 + 1 的情况也满足:
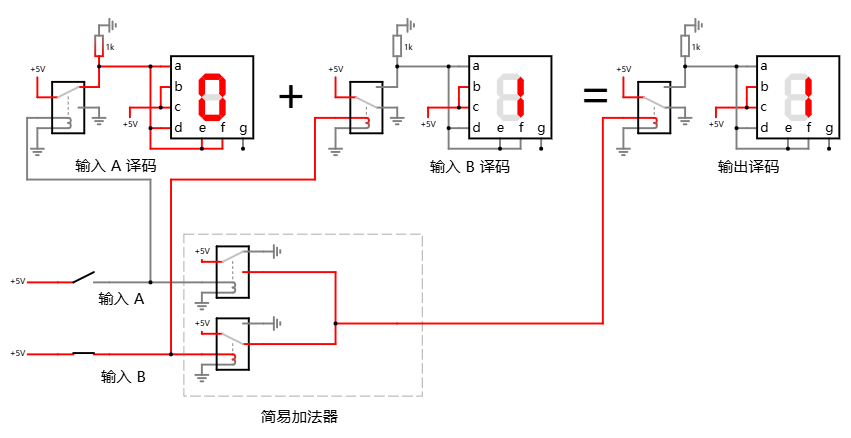
最后, 1 + 0 也同样满足, 于是三条加法规则都同时得以实现:
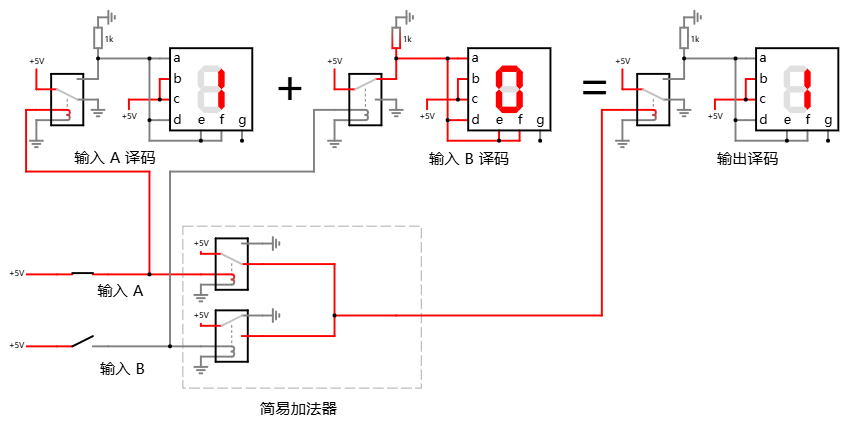
继电器并联实现前三条规则 在线可互动操作示例
当然, 最后一种 1 + 1 的情况依然是不行的.
单独由两个继电器构成的并联的四种状态如下:
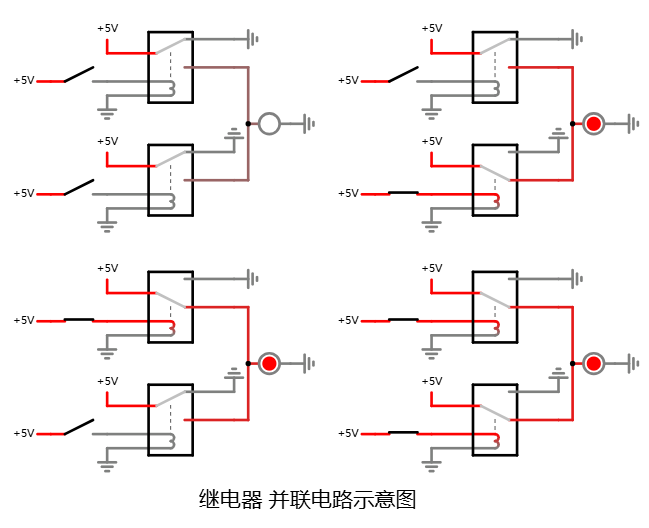
并联逻辑的继电器实现, 四种情况 在线可互动操作示例
初看上去, 这个并联实现的加法器方案要复杂的多. 但首先, 它解决了所谓的电流倒灌问题, 现在输入 A 和输入 B 之间根本就无关联, 两个输入是两个独立的回路, 无需使用二极管, 谁也不会影响谁;
其次, 输出也不是从输入那里来的, 它也是一个独立的回路, 由一个内部的电源去输出的. 输入只是表现为一种间接的控制手段.
这种间接性是很有用的. 如果说前面的并联电路逻辑还能简单通过直连的直接方式实现, 那么如果要实现一个串联电路的逻辑呢?
也即是两个只要有一个是低电平, 输出就是低电平; 只有两个都是高电平时, 输出才是高电平:

串联电路的四种情况 在线可互动操作示例
通过继电器的间接控制方式, 是很容易想到下述实现的:
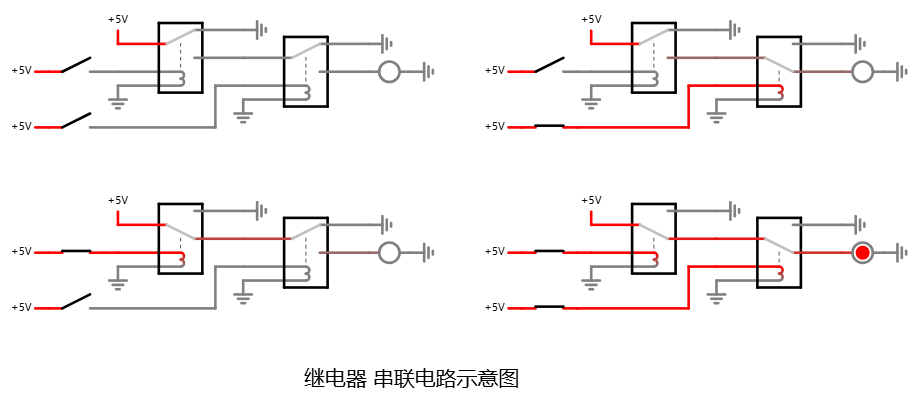
串联逻辑的继电器实现, 四种情况 在线可互动操作示例
而如果想像前面那种二极管方案的直连方式去实现这个串联逻辑, 要怎么去做呢? 反正我是没有想到, 如果你能想出来, 欢迎你告诉我.
当要表达的逻辑越来越复杂时, 没有间接控制的手段, 表达起来会越来越困难, 甚至不可能.
最后, 上述的解决方案也依然遗留了 1 + 1 = 1 的问题, 而我们要的是 1 + 1 = 2. 当我们人类想表达一个人很笨时, 有时会这样说: "他连 1 + 1 = 2 都不会." 似乎 1 + 1 = 2 是一个再简单不过的问题.
不过在这里, 显然, 1 + 1 = 2 并没有那么简单, 0 + 0 才是最简单的, 不管是多么复杂的计算机也好, 计算器也好, 它必然也要能做 0 + 0 = 0, 以及 0 + 1 = 1 和 1 + 0 = 1.
反之, 一个能做复杂运算的计数器, 如果这几个简单的加法反而算不对的话, 也不算是个合格的计数器.
不要认为目前做的工作太简单了, 没有意义, 至少我们熟悉了一些电路器件的特性, 我们也能表达类似 反向, 串联, 并联 等逻辑, 也初步熟悉了模拟器的使用, 这为后面解决更难的问题打下了良好的基础.
接下来, 将开始挑战一个真正有难度的规则, 也即是 1 + 1 = 2, 看看用一堆电路到底要怎么去实现它.