通过真值表构建全加器
全加器的原型如下:
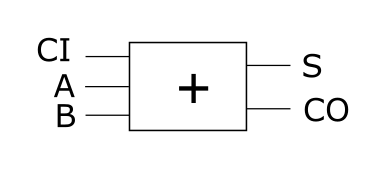
- 三个输入 A, B, CI;
- 两个输出 CO, S.
通过真值表构建全加器的过程的第一步是列出真值表, 三个输出总共 8 种不同组合:
| A | B | CI | CO | S |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
CO 输出
依然是分成两个部分分别去处理. 第一块是 CO 方面:
| A | B | CI | CO |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
留下为 1 的部分:
| A | B | CI | CO |
|---|---|---|---|
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
得出表达式:
CO = A'·B·CI + A·B'·CI + A·B·CI' + A·B·CI
依据逻辑代数相关定律, 可以进一步化简:
CO = A^B·CI + A·B
注:
^表示求 异或对化简过程有疑问的, 请参阅前面相关章节.
S 输出
第二块是 S 方面:
| A | B | CI | S |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
留下为 1 的部分:
| A | B | CI | S |
|---|---|---|---|
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 |
得出表达式:
S = A'·B'·CI + A'·B·CI' + A·B'·CI' + A·B·CI
依据逻辑代数相关定律, 可以进一步化简:
S = A'·B'·CI + A'·B·CI' + A·B'·CI' + A·B·CI
= A'·(B ^ CI) + A·(B'·CI' + B·CI)
= A'·(B ^ CI) + A·(B ^ CI)' // 注: B'·CI' + B·CI 实际就是所谓的 同或 模式, 是 异或 的反模式. 证明见下文.
= A'·T + A·T' // 令 T = B ^ CI
= A^T // 异或逻辑
= A^(B^CI) // 展开, 最终可以使用一个三输入异或门
异或 和 同或 取反关系的一个证明:
(B ^ CI)'
= (B·CI' + B'·CI)' // 异或逻辑展开
= (B·CI')' · (B'·CI)' // 德摩根定律
= (B'+CI) · (B+CI') // 德摩根定律
= B'·B + CI·B + B'·CI' + CI·CI' // 分配律
= 0 + CI·B + B'·CI' + 0 // 互补律
= CI·B + B'·CI' // 0 + A = A
= B'·CI' + B·CI // 交换律, 得证.
多输入异或门本质上是一个 奇偶发生器(Parity Generator), 当多个输入中有 奇数 个 1(高电平) 时, 输出为 1(高电平).
你可以通过前述 S 的真值表验证这一点.
对于普通的(二输入)异或门, 这点依然成立.
门电路图
综合两部分表达式, 可以得出最终的门电路实现:
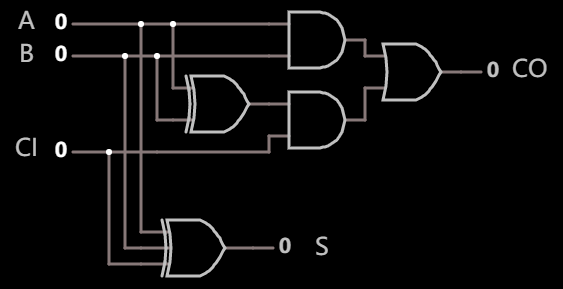
经测试, 是可以满足要求的:
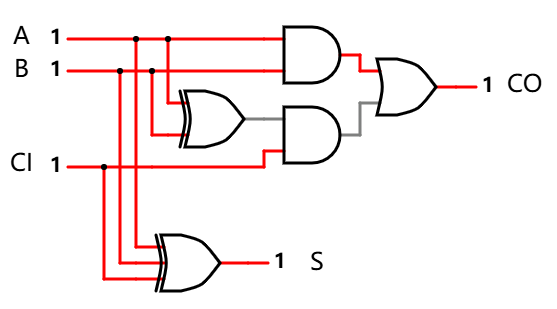
注: 以上只截取了相加等于 3 的一个示意图, 其它图从略, 读者可以自行验证.
通过 创建子电路 的方式还可以进一步封装成为自定义的子电路, 不过, 因为模拟器本身就已经内置了该模块, 这里就不去做这个操作了. 读者有兴趣的可以自行封装下, 也算是对 创建子电路 功能的一次巩固练习.
线上电路原型
最后, 给出本文用到的示例电路: