通过门电路实现三位 LED 译码器
在前面, 通过继电器及二极管等方式曾实现了一个简易的译码电路, 能够在 LED 数码管上显示 0, 1 和 2.
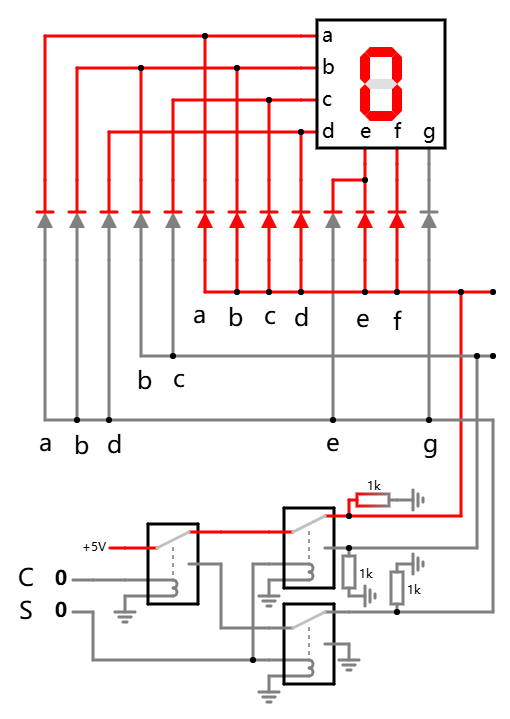
通过分而治之的方式, 有了另一种实现:
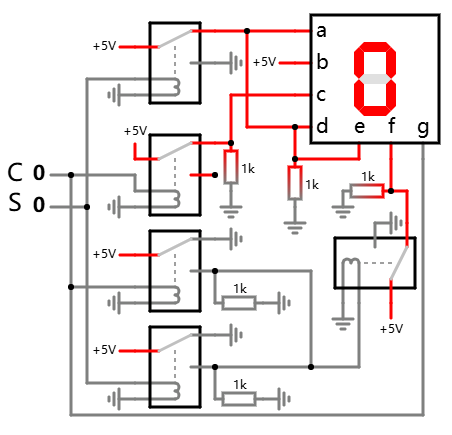
这些实现都极大依赖仔细的分析, 观察, 思考以找到规律并简化, 但最终也仅仅只是能显示三个数字而已.
当然也是可以考虑实现更多数字的显示的, 但恐怕就麻烦不少了.
现在, 运用前述通用的机械公式方式及门电路, 来看看怎么实现它. 而且, 我们打算不止是显示 0, 1, 2, 而是一直显示到 7, 也即总共有 0~7 8 不同个数字.
如此一来, 输出的线路也需要从两根扩展到三根, 三根线正好可以表达 8 种状态.
真值表
第一步依旧是根据 LED 显示 0~7 的要求列出 a~g 对应的二进制数:
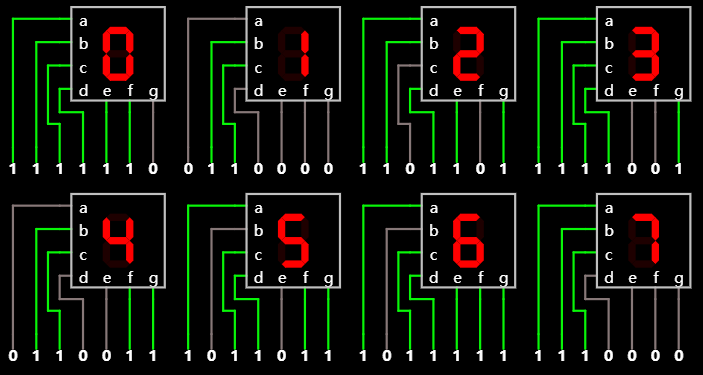
LED 数码管显示 0~7 所对应的输入组合 在线可互动操作示例
然后, 真值表如下, A, B, C 代表输入(同时也即是加法器的输出, 在译码电路中则作为输入); a, b, c, d, e, f, g 代表输出:
| A | B | C | a | b | c | d | e | f | g |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
之后, 依旧是按照拆分的方式, 当然, 这次因为一方面输出的规则众多(8条规则), 另一方面输入也更多(三个), 像之前那种简单找规律已经不太灵光了, 我们也不打算再去仔细观察输入输出的规律, 就按机械方式来处理.
其实, 现在也很难找到什么规律, 比如 a-g 也没有完全一致的了, 单纯依靠一个输入就能决定的输出也很难去观察到(我也没有一一去仔细观察, 但现在数量如此之多, 想找到这种情况肯定更难了)
a 段
先看第一段 a 的情况:
| A | B | C | a |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
有 6 个为 1 的情况, 为 0 的只有两个. 前面说要找到那些为 1 的, 但目前的情况, 为 1 的太多, 为 0 的更少, 其实我们也可以反过来求出 !a, 最后再把结果反过来即可:
| A | B | C | a | !a |
|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 0 |
如此一来, !a 只有两条为 1 的情况:
| A | B | C | a | !a |
|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 |
一个是 001(数字 1), 一个是 100(数字 4), 据此, 可以写出表达式:
(!A · !B · C) | (A · !B · !C)
当然, 这个结果是 !a, 要得到 a, 再取一次反即可:
!((!A · !B · C) | (A · !B · !C))
取反的情况很多, 为减少非门的使用, 可以考虑应用 德摩根定律, 可以进一步化简:
!((!A · !B · C) | (A · !B · !C))
= !(!A · !B · C) & !(A · !B · !C) // 德摩根定律
= (A | B | !C) & (!A | B | C) // 德摩根定律
这样只有两处要取反, 据此, 即可画出对应门电路如下:
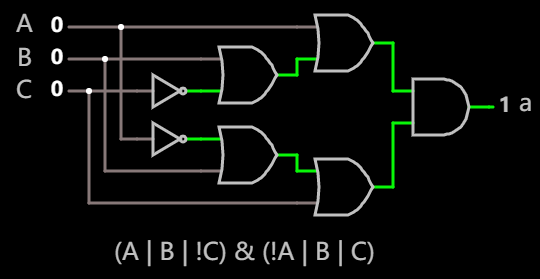
显示 a 段的逻辑电路 在线可互动操作示例
使用多输入门电路化简
因为有三个输入端, 这里用了两个 或门, 并把第一个或门的输出作为第二个或门的输入, 从而实现对三个输入 A B C 取或的操作.
显然, 即便有更多的输入, 不过是级联更多的门罢了, 问题总是可以解决的.
不过对于此种情况, 还有一种更简便的方式, 就是使用 多输入门电路.
在上述或门上双击(或 右键--属性), 在弹出的编辑属性窗口中, 找到 #输入 输入项, 把缺省的数字 2 改为 3, 即可调整为 三输入或门:
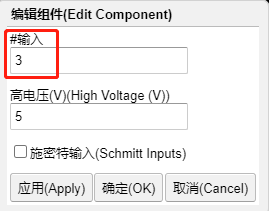
显然, 如果有更多输入的情况, 不过是把这个数字改为更大而已.
最终, 简化的电路如下:
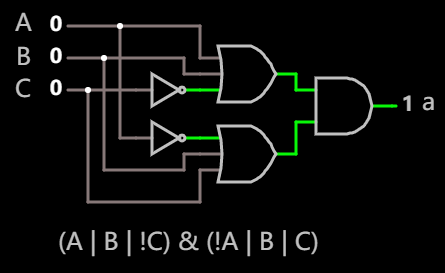
显示 a 段的逻辑电路(使用三输入或门) 在线可互动操作示例
三输入的或门可以认为它内部封装了两个或门, 并以前述方式把第一个或门的输出作为第二个或门的输入连接起来, 最终暴露给我们的接口就是三个输入, 一个输出.
同理, 与门, 与非门, 或非门 乃至 异或门 都支持这种多输入的调整.
注意: 关于两输入 异或门, 我们先前说它能判断两个输入是否相同, 不过对于多输入异或门而言, 它的行为逻辑不是判断输入是否相同, 而是多个输入中是否含有 奇数 个 1(高电平).
这一结论对于两输入异或门同样成立, 所以异或门也常用于奇偶性判断.
你可以手动级联两个两输入异或门, 然后观察它的行为即可知道, 或者列举一下真值表也行.
根据逻辑代数定律进一步化简
在之前, 得到了一个 a 段的最终逻辑表达式为 (A | B | !C) & (!A | B | C), 我们说它是一个简化的结果, 但其实它还不是最简的.
清点一下, 不难发现, 这个逻辑式需要两个 非门, 两个三输入或门, 最后还要一个 与门 将结果综合起来, 也即总共 5 个门电路.
如果想进一步的化简, 就需要知道一些逻辑代数方面的定律, 我们前面也谈到了不少, 比如 德摩根定律, 还有交换律, 结合律, 互补律等.
为叙述的方便, 这里引入一种新的关于 与或非 的表达方式.
取反的新表达
常规的方式是 !A, 新的方式用 A', 也即是后接一个单引号;
取或的新表达
常规的方式是 A | B, 新的方式用 A + B, 因为 逻辑或 也叫 逻辑相加;
取与的新表达
常规的方式是 A & B, 新的方式用 A · B, · 表示 乘号, 因为 逻辑与 也叫 逻辑相乘;
最后, 乘号一般可以省略, 最终可以简写为 AB. 对于多个输入的情况, 这样会简化很多, 也不用使用太多括号.
具体化简例子
有了上述新的表达, 对于 a 段的逻辑表达式 (A | B | !C) & (!A | B | C), 可以写成:
(A+B+C')(A'+B+C)
然后, 逻辑代数有所谓 交换律, 交换一下, 得到:
(B+A+C')(B+A'+C)
这个交换的结论是很明显, 几乎无需证明.
然后, 逻辑代数还有 结合律:
- A(BC)=(AB)C
- A+(B+C)=(A+B)+C
以及 分配率:
- A(B+C)=AB+AC
- A+(BC)=(A+B)(A+C)
注意: 以上 A B C 既可以是单个的值, 也可以是一个复合的表达式.
这些的正确性都可以得到证明, 最简单的证明方式就是枚举出真值表, 一对比即可知.
应用 分配率, 对于前述表达, 可有:
(B+A+C')(B+A'+C)
=B+(A+C')(A'+C) // 分配率第二条反过来运用, 提取公共的 B
=(B'((A+C')(A'+C))')' // 德摩根定律, 将 (A+C')(A'+C) 视为一个整体
=(B'((A+C')'+(A'+C)'))' // 德摩根定律
=(B'(A'C+AC'))' // 德摩根定律
=(B'(A⊼C))' // 注: A'C+AC' 就是 异或, 符号 `⊼` 表示异或操作.
最终结果是 A 和 C 取异或, 再与 B 的反 取与非.
也即需要一个 异或门, 一个 非门 和一个 与非门 总共三个门电路.
最终 a 段的电路可以进一步简化为:
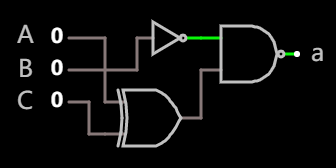
e 段
再举另一个例子, e 段,
| A | B | C | e |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
为 1 的有三段:
| A | B | C | e |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 1 |
据此, 得出 A'B'C'+A'BC'+ABC' 的表达式.
其化简过程如下:
A'B'C'+A'BC'+ABC'
=A'C'B'+A'C'B+ABC' // 交换律
=A'C'(B'+B)+ABC' // 分配率
=A'C'(1)+ABC' // 互补律
=A'C'+ABC' // 1·A=A, 1 与 任何值 A, 结果就是 A.
=C'A'+C'AB // 交换律
=C'(A'+AB) // 分配率
=C'(A'+B) // 逻辑代数公式: A+A'B=A+B, 证明见下文.
=(C+(A'+B)')' // 德摩根定律, 此处为减少非门的数量, 最后整体可以使用一个 或非门
=(C+AB')' // 德摩根定律
注: 上述用到一个逻辑代数公式:
A+A'B=A+B. 如果不清楚为何是这样, 最简单的方式就是枚举所有情况, 因为 A 的情况无非也就两种: 0 或 1.
- 假如 A = 0, 左边
A+A'B=0+1·B=0+B=B, 右边A+B=0+B=B, 左边等于右边;- 假如 A = 1, 左边
A+A'B=1+0·B=1+0=1, 右边A+B=1+B=1, 左边等于右边;综上, 得证.
上述证明用到下述特性, 也是也显然无需证明的:
- 0·A=0
- 1·A=A
- 0+A=A
- 1+A=1
另, 此公式稍微变形即可得到:
A'+AB=A'+B, 上面推演过程即应用了此变形.
最终, 需要一个 非门, 一个 与门, 一个 或非门 总共三个门电路.
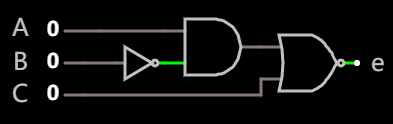
显示 a 和 e 段的最简逻辑电路 在线可互动操作示例
遵循相同的步骤, 可以得出剩余的 5 段所需的电路, 具体的过程这里不一一展开, 最终的一个结果如下:
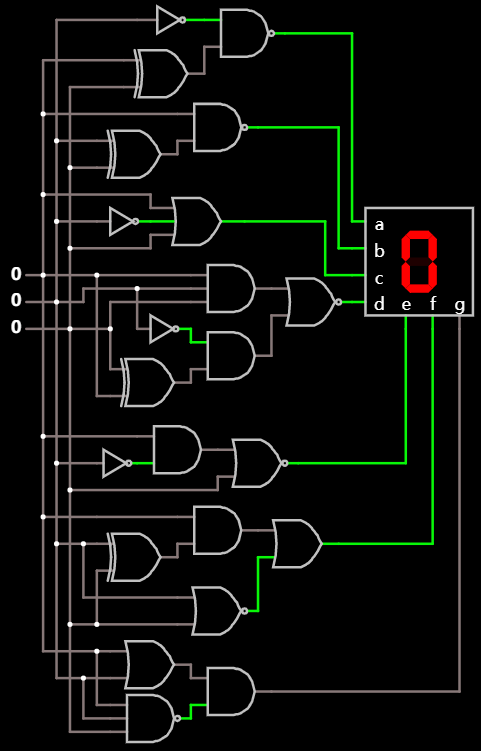
这里有些电路或许也还不是最简的. 想要知道更多逻辑代数方面的公式与定律, 请参考相关教科书.
另: 除了公式化简法外, 其它一些化简方式还有:
- 卡诺图化简法(Karnaugh Map)
- 奎恩-麦克拉斯基化简法(Quine-McCluskey, 也称 Q-M 法)
读者可自行去了解, 这里不一一介绍.
显示一个先前未曾实现过的数字 4 的情况:
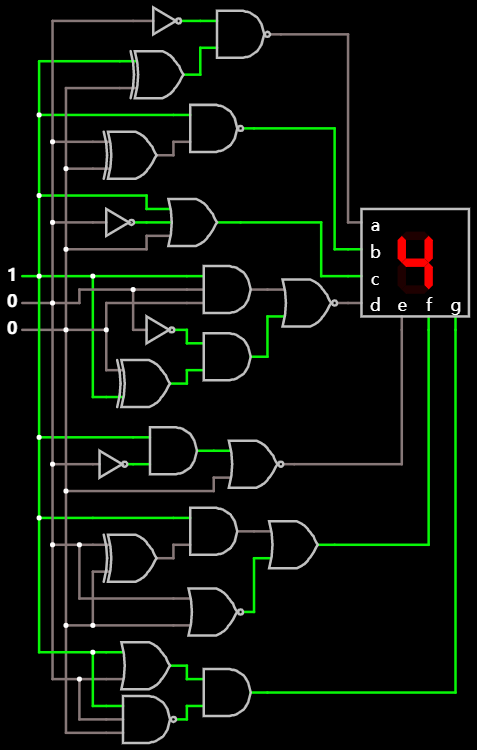
LED 译码电路 线上模拟器可互动操作示例
事情至此也面临一个新的问题, 那就是整个电路非常之庞大(尽管已经一再简化). 假如后续还要塞入运算的部件, 还有显示两个加数的模块, 整个屏幕恐怕都无法显示.
在之前, 我们一直都有看到封装与抽象的威力及带给我们的好处, 比如 三输入或门 就封装了两个或门在其内部, 使得可以很简便地得到想要的功能.
更基础的, 如各种门电路, 都是对各种底层的继电器(或是晶体管)逻辑电路的封装.
假如没有这些门电路的封装, 目前实现的这个译码电路恐怕还要更为复杂. 现在的问题是, 能否进一步的去抽象与封装这个译码电路呢? 假如可以, 就可以把这一大堆组件及连接的细节隐藏到一个新的模块的内部, 后面想把两个加数与和都显示出来就简单了.
而这就要涉及到模拟器的一个新的功能: 创建子电路. 在下一章节, 将以译码电路为例, 探讨这一主题.