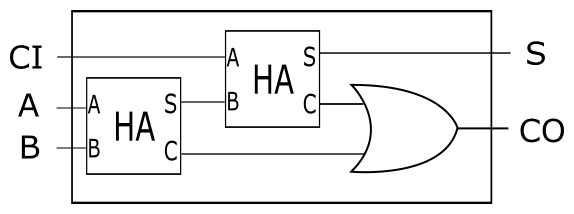
通过半加器构建全加器
构建全加器的另一种方式是通过半加器. 为方便叙述, 还是使用我们更为熟悉的十进制.
但底层的道理是一样的, 讨论的结果同样适用于二进制.
具体例子
考察一个例子: 7+8+1(1 代表一个进位输入), 最终结果是 16, 要得到一个 6 和一个新的进位.
既然实质就是做两次两个数的加法, 那么作为一种简单粗暴的方式, 依旧是弄它两个半加器, 然后连起来, 代表两次加法:
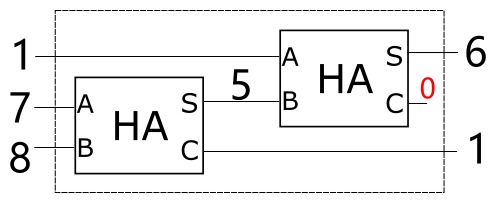
在这里, 第二个半加器的进位输入被我们丢弃了, 只取了第一个的进位作为最后输出.
对上述例子而言, 目前的做法显然是 OK 的, 但能否适应更一般的情况呢? 让我们来看另一个例子: 4+5+1
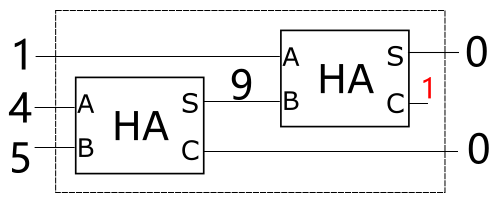
结果悲剧了, 应该是 10, 但输出却是 00, 在第二个半加器里才出现了进位, 但被丢弃了, 导致了错误的结果.
由于无法预料会在哪里产生进位, 丢弃哪一个都不行. 简单的处理就是再引入一个半加器, 把这俩再加一下:
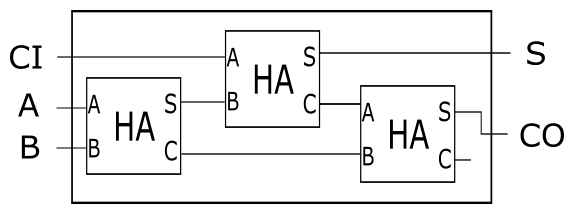
注: 是把第三个半加器的加位作为最终的进位输出, 进位则丢弃(最终只需要两个输出, 势必要丢掉一个).
如果我们观察一下人做加法的一般过程, 那么我们的确是在不知不觉中做了三次两个数的加法:
现在考察以下两种情况, 都能够满足要求:


两次进位的问题
现在, 即便前面两个都产生了进位, 1+1=2, 第三个半加器结果最大也不过是 2, 要满 10 才能产生进位, 因此, 丢弃它的进位是安全的.
但另一方面, 最终的进位输出(CO)可能会参与到下一级的进位输入(CI)中去, 比如前面构建多位加法器时:
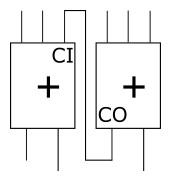
如果真的产生了两次进位, 则违反了我们关于进位输入只能为 1 或 0 的假设.
仔细审查一下, 我们可以断言, 如果进位输入满足了假定, 两个半加器都产生进位的情况是不存在的.
因为这意味着三个数之和至少达到了 20!
考虑其中的进位输入最大也就是 1, 三个数最极端的情况也就是 9+9+1=19, 不可能超过 20.
因此, 只要一开始没有违反进位输入(CI)的假定, 那么进位输出(CO)也是可控的, 因此级联多个一位全加器组成多位加法器是可行的.
这一结论同样适用于二进制.
三个二进制一位数数相加, 最大就是 3, 也就是 1 + 1 + 1 的情况.
如果产生两次进位, 而因为一次进位就表示结果至少到了 2, 两次就是 4, 超过了 3, 是不可能的.
对进位逻辑的再思考
综上所述, 进位或者来自第一个半加器, 或者来自第二个半加器;又或者都没有进位, 但不可能同时产生进位!
概括地讲, 第三个半加器只需处理这三种情况:
- 0+0 --> 0;
- 0+1 --> 1;
- 1+0 --> 1.
它甚至不用处理我们通常认为最简单的 1+1.
这对于一个我们设想能够处理任何两个个位数相加的半加器来说, 的确是有点屈才了, 从它的进位输出被丢弃也可看出它没有得到充分利用.
事实很明显: 这里的逻辑其实无需用一个半加器去实现.
到目前为止, 我们的全加器由三个半加器构成:

它是能够满足我们的要求的, 但我们希望或许能够简化并用一个更简单的器件代替第三个半加器:

显然, 上面实际上只使用了半加器里的 S 的输出作为 CO 的最终值. 而我们知道半加器里面可以分为两部分, 负责 S 输出的就是一个 异或门, 因此这里可以直接只用异或门即可.
当然, 再度仔细分析下, 上述三种情况, 甚至连异或门都不是必要的, 一个 或门 就足够了, 因此, 最终一个全加器可以由两个半加器再加一个或门构成: