一般性的加法过程
现在来考察一下一般性的加法过程, 因为我们更为熟悉十进制, 这里就用十进制来讨论, 但这些原理同样适用于二进制.
无进位做加法的过程
从一般的情况出发, 比如怎么计算 24+35 呢? 有三步
- 把个位与个位相加, 4+5=9;
- 再把十位与十位相加, 2+3=5;
- 再合起来得到 59.
自然, 这是没有进位的情况, 一切都没有问题, 如果我们有十进制的一位加法器原型, 那么用两个并列就能完成这个过程了:

有进位做加法的过程
但事情往往不会那么简单, 现在再考虑另一组加法: 256+128. 通过组合三个一位数加法器, 分别处理个位, 十位与百位数字的相加, 结果如下:

显然, 3714 不是我们想要的结果, 因为没有考虑到进位的影响, 正确的结果应该是 384.
所以现在需要修正一位加法器的原型:
首先至少要两个输出, 一个是 加位(sum,S) 的输出, 一个 进位(carry,C) 的输出, 这点我们在前面就已经明确过:
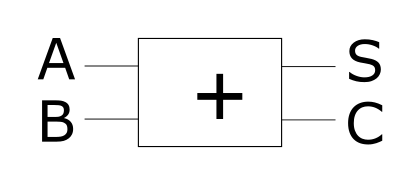
其次, 进位 的输出还要参与到下一级的输入中去, 也即要有 三个 输入, 输出则只要显示 加位 的结果即可:

对于右边最低位, 不存在进位, 使用一个接地符号表示输入为 0;
其余的进位输入则来自低位的进位输出;
图中红色的线表示产生了进位: 对于中间的十位数加法, 实际是 5+2+1=8.
经过这样的调整, 多位加法器就能正常工作了, 但这样一来, 模型也复杂多了.