通过 与非门 构建异或门
构建异或门的方式可以有多种, 因此, 采用 与非门 去构建最终的异或门的方式也同样有多种.
基本门电路方式
在之前, 通过 与门, 与非门和或门, 我们已经成功构建过 异或门.
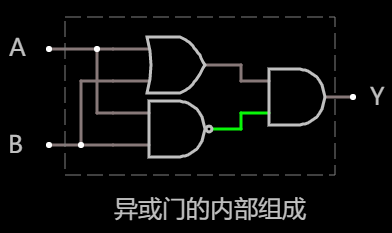
另外, 我们也知道 与门 和 或门 均可以通过 与非门 构建出来, 因此依样替换, 即可得到一个全部由 与非门 构成的 异或门:
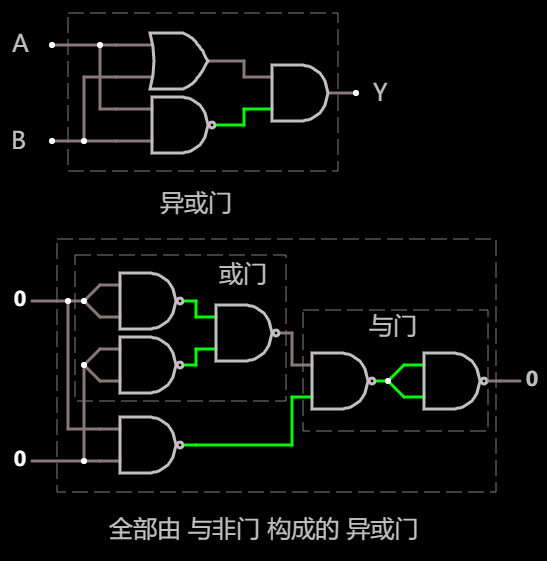
全部由 与非门 构成的 异或门 在线可互动操作示例
不过这样构建出来的异或门实际上还不是最优的, 清点一下, 我们发现, 这个电路总共用了高达 6 个 与非门.
真值表套公式方式
此外, 前面另一种通过套公式的机械法也能实现异或门:
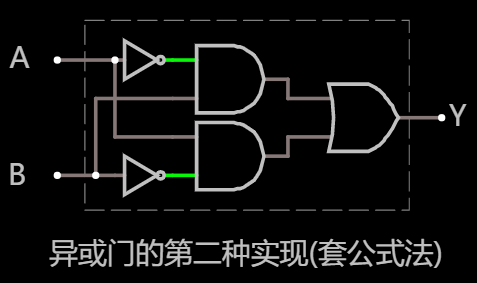
将这里的与门, 或门 和 非门全部使用 与非门 替代, 最终如下:
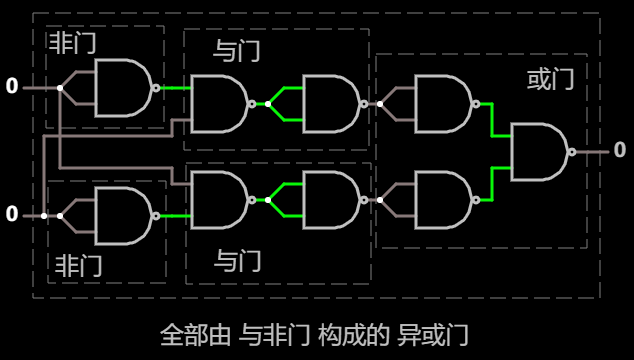
异或门第二种实现, 展开为 与非门 在线可互动操作示例
总共高达 9 个与非门, 不过, 不难注意到两处的取反是可以抵消的, 据此, 可以简化:
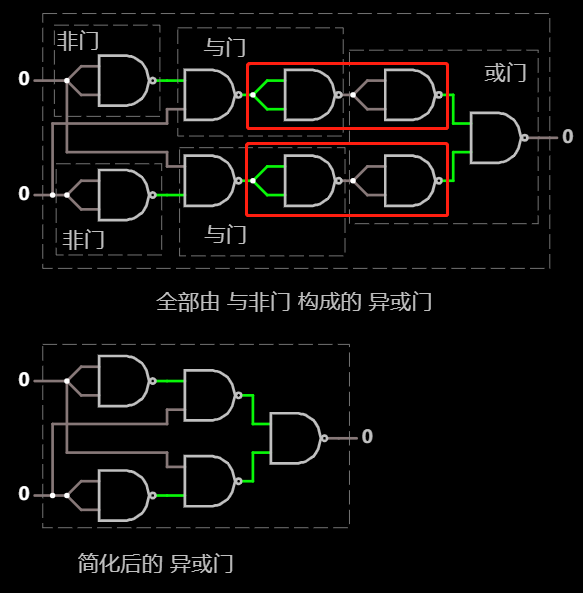
异或门第二种实现, 展开为 与非门, 简化后 在线可互动操作示例
这样一来, 只用 5 个 与非门 即可实现 异或门 的逻辑, 比前面 6 个的方案还少了一个.
可以验证它确实是满足异或门真值表的, 具体展示此处从略.
逻辑代数推演的最优方式
不过呢, 以上还不是最简化的方案! 其实如果你仔细观察上述 5 个与非门构成的简化版本的最左侧的输入部分, 不难发现它们两个输入上下是对称的, 两个与非门存在一定的重复.
最优化的实现可消除输入部分的重复, 只需要 4 个与非门:
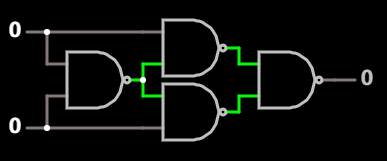
全部由 与非门 构成的 异或门 在线可互动操作示例
可以验证, 它也符合异或门的真值表.
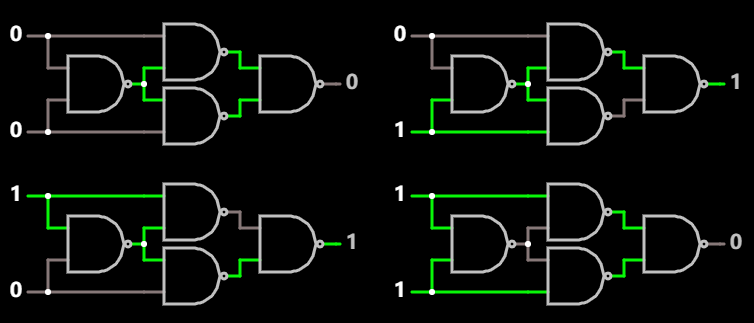
全部由 与非门 构成的 异或门, 四种情况 在线可互动操作示例
这样的一个实现很简洁, 并且具有对称的美感.
逻辑代数的一些基本定律
从套公式法得到的异或门表达式 Y = (!A & B) | (A & !B) 出发, 根据逻辑代数方面的一些定律, 可以推出这个结果. 这些定律包括:
- 还原律
- A = !!A, 两次取反, 结果等于原值.
- !!A = A, 两次取反, 互相抵消.
- 德摩根定律
- !(A & B) = !A | !B
- !(A | B) = !A & !B
- 分配率
- A & (B | C) = (A & B) | (A & C)
- A | (B & C) = (A | B) & (A | C)
- 互补率
- A & !A = 0, A 和 !A 必有一个为 0, 求与 后必为 0.
- A | !A = 1, A 和 !A 必有一个为 1, 求或 后必为 1.
注: 以上, A 和 B 可以是单个值, 也可以是一个复合的表达式.
这些定律的正确性, 有些是比较明显的, 有些不好理解的, 读者可自行绘制真值表验证. 证明从略.
逻辑代数的其它定律请参考相关教科书.
推理过程
具体的推理过程如下, 脱字符 ^ 表示 求异或 运算, ⊼ 表示 求与非 运算. 运算优先级方面, 求反 最高, 其次 求与(逻辑相乘), 其次 求或(逻辑相加).
A^B = (!A & B) | (A & !B)
= !!(!A & B) | !!(A & !B) // 两次取反, 结果不变
= !(!!A | !B) | !(!A | !!B) // 德摩根定律
= !(A | !B) | !(!A | B) // 两次取反, 互相抵消
= !( (A | !B) & (!A | B) ) // 德摩根定律
= !( (A & !A) | (A & B) | (!A & !B) | (B & !B) ) // 分配率
= !( (A & B) | (!A & !B) ) // 互补律, A & !A = 0, B & !B = 0, 以及 0 | A = A
= !(A & B) & !(!A & !B) // 德摩根定律
= !(A & B) & (!!A | !!B) // 德摩根定律
= !(A & B) & (A | B) // 两次取反, 互相抵消
= (!(A & B) & A) | (!(A & B) & B) // 分配律
= !!((!(A & B) & A) | (!(A & B) & B)) // 两次取反, 结果不变
= !((!(!(A & B) & A)) & (!(!(A & B) & B))) // 德摩根定律
= !((!((A ⊼ B) & A)) & (!((A ⊼ B) & B))) // 与非替代, A ⊼ B = !(A & B)
= !((!(T & A)) & (!(T & B))) // 令 T = A ⊼ B, 等价替换
= !((T ⊼ A) & (T ⊼ B)) // 与非替代
= (T ⊼ A) ⊼ (T ⊼ B) // 与非替代
最终, (T ⊼ A) ⊼ (T ⊼ B) 里面有三次 与非 过程, 加上 T = A ⊼ B 里的一次 与非 过程, 总共需要四个 与非门 即可, 也即得到上述的电路.
读者可以自行验证其逻辑.