用更多的位来表示 2

最后, 回到如何表示 2 的问题上, 我们前面之所以没办法表示 2, 很显然, 主要的问题在于加法器的原型设计里, 输出只有一根线.

就像你只有一个人, 一个单身汉或者一个单身妹, 虽然也能吃能喝, 但想干更多的事, 比如生个崽啥的, 那一个人就不行了, 得两个人.

如果你再观察我们做加法的许多情况, 比如 5 + 7 = 12, 其实这里它的返回 12, 你也可以认为它不是一个数, 而是由两个数 1 和 2 构成.

你完全可以认为它返回了两个数, 当然因为你已经习惯了多位数, 而且它们挨在一起很近, 你受到的教育告诉你, 应该把它们看作一个整体, 是一个数 "十二", 而不是两个数 一 和 二.

但如果给一个刚学会 0-9 十个数字的小孩子看呢, 他还不知道什么是 多位数, 他就会认为这里是两个数, 甚至认为 12=3 也不奇怪.

在设计加法器时, 同理, 没有人规定你只能用一根线做返回, 我们没必要把自己困死在一根输出线上.

有句话怎么说的? 不要在一颗树上吊死自己...多找几颗树试试, 相信我, 一定也可以吊死的...

也因此没必要在 更高电压, 更更高电压 上做文章, 这有点像是逮着一只羊, 眼里就只有这一只羊, 然后使劲去薅它羊毛, 那很容易把它薅秃噜毛了.

多找几只羊, 多整几根线, 事情就豁然开朗. 现在先调整一下加法器的原型, 给它整两根输出线:

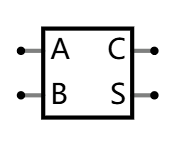
输入端 A 和 B 不变;

两个输出端 C 和 S.

C 和 S 的具体含义后面再解析.

规定一个从上到下, 从左到右, 从高到低的顺序, 两根线一起的输出排列起来可以有四种状态:

C S
-----
低低=0;
低高=1;
高低=2;
高高=3;

就足以表达 0, 1, 2, 3 四个数字, 状态不足的问题解决了, 表示的问题没有了, 甚至还能多表达一个数字 3. 但怎么去显示的问题又出来了, 还有更重要的, 怎么去设计这个新的运算电路.

这一次, 先把显示的问题搁一边, 因为这不是核心的问题, 而且它必须建立在正确的输出之上, 需要优先解决的是输出的问题.

另一方面, 模拟器本身已经为输出不同电平显示了不同的颜色, 足够让我们区分不同状态了.

在更进一步分析这个加法器的设计前, 需要涉及一个新的问题, 也就是所谓的 二进制 的问题. 既然都已经讨论到这一地步, 也是时候把它介绍给大家了, 同时也为后续的讲解带来方便.