半加器的分解
始终, 分而治之是一以贯之的一个策略, 如果要处理的问题比较棘手, 那么就考虑如何进行功能抽象并把它们分解, 这是应付复杂性的一个重要手段.
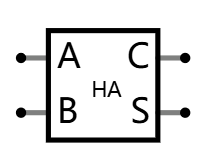
比如, 输入能否分解呢?
你有两个输入, 但一次只考虑一个输入的话, 你既不能确定进位的结果, 也不能确定加位的结果, 所以你是不能分的. 通常而言都不会考虑分解输入.
那么, 两个输出又能否分解呢? 我们注意到两个输出, C 和 S 都可以表示成输入的 函数(Function):
C=f(A, B)
S=f(A, B)
注: 如果你不太了解函数, 这里可以简单理解为 C 和 S 的值都可以通过 A 和 B 来得到.
完全由输入所决定, S 与 C 无关, C 也与 S 无关, 它们均由 A, B 决定:
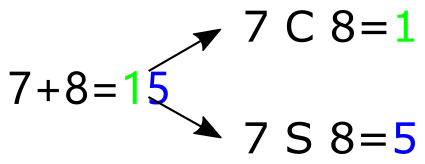
比如, 在上图中, 引入 C 和 S 作为两个运算符, 代表 进位 运算和 加位 运算.
就像
+和-分别代表加法和减法那样.
对于进位运算, 有:
2 C 3 = 0;
6 C 1 = 0;
5 C 5 = 1;
7 C 8 = 1;
最后的结果就是进位, 为 0 就表示没有进位, 为 1 就是有进位.
注: 这里用的是十进制, 但道理是一样的.
显然, 给定了两个输入的值, 就能确定是不是能产生进位, 至于加位那边是什么结果, 则与这里无关.
同理, 对于加位运算, 有:
2 S 3 = 5;
6 S 1 = 7;
5 S 5 = 0;
7 S 8 = 5;
代表最终加完后丢弃进位的结果. 所以才有 2 S 3 = 7 S 8, 因为最终的结果都是 5.
同样的, 给定了两个输入的值, 就能确定加位的结果, 至于能否产生进位, 则同样与这里无关.
另, 如果你不习惯这样的表达, 也可以把它们写成两个自变量的函数形式:
S(2, 3) = 5;
S(6, 1) = 7;
S(5, 5) = 0;
S(7, 8) = 5;
C 同理, 这里不再一一写出.
其实, 加减法本质上也是两个变量的函数, 函数名就是
+和-, 然后有:+(2, 3) = 5; +(7, 8) = 15; -(6, 2) = 4; -(3, 9) = -6; ...等等.只是这些函数太常用, 我们一般把它们写成特殊形式, 如
2 + 3和6 - 2, 但这些不过是形式层面的差别.
据此, 我们可以在内部把输入同时传递给两个部件并因此拆解两个输出, 分成一个 进位器 和一个 加位器 两部分:
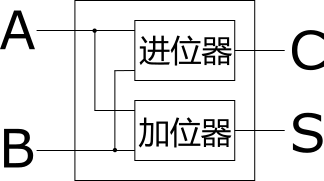
根据前面整理的需求:
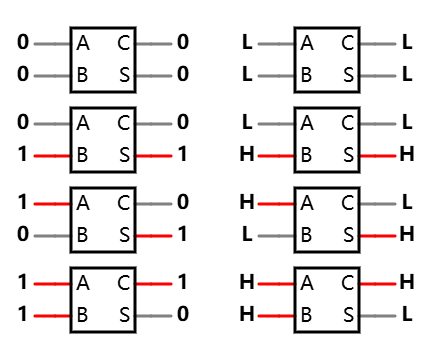
可以把整体的输入输出关系列举成下述的表:
| A | B | C | S |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
这也就是所谓的 真值表(Truth Table). 它表达了输入和输出间的关系.
而所谓 进位器 就是上述的把加位 S 的输出去掉后的一个子表:
| A | B | C |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
而所谓 加位器 就是把进位 C 的输出去掉后的另一个子表:
| A | B | S |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
我们的任务就是设计两个组件, 进位器和加位器, 使之分别能够满足上述的约束.
如果用软件语言来表达, 大概是这样:
public Output halfAdd(Input a, Input b) {
Sum s = sum(a, b);
Carry c = carry(a, b);
return new Output(s, c);
}
public Sum sum(Input a, Input b) {
// TODO
return null;
}
public Carry carry(Input a, Input b) {
// TODO
return null;
}
如果你没有编程的基础, 可暂时忽略这里.
尽管我们还不知道它们工作的细节, 但已经可以单独拿出比如"进位器"模块来分析:

通过这样拆分输出的方式, 又回到了两个输入, 一个输出的简单原型上, 而且可以一个一个的加以解决.