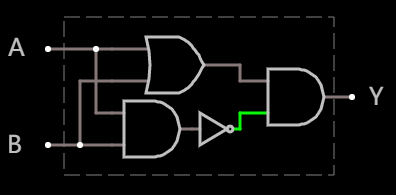
通过 与门, 或门, 和 非门 构建 异或门
在前面, 异或门或者通过跷跷板式的电路实现, 或者直接就是一个模拟器的内置组件, 其内部实现是一个黑盒, 我们不得而知.
我们说, 与门, 或门 和 非门 是最基本的门电路, 而异或门是组合的门电路, 换言之, 可以通过组合那些基本的门电路来构成, 那么要怎么去组合呢?
对比现有的门电路
现有的三种基本门电路, 以及经它们简单组合形成的 或非门 和 与非门, 列举其真值表, 然后与 异或门 的进行对比, 不难发现, 有两种门电路比较接近 异或门 的逻辑.
首先, 异或门的真值表如下:
| A | B | Y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
一个比较接近的是 或门, 将其真值表与 异或门 的对比下, 不难发现, 就差最后一项:
| A | B | Y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
或门 最后一项的值是 1, 但 异或门 要求的是 0, 因为 1 + 1 产生了进位, 进位后就归零了.
另一个比较相似的是 与非门, 对比一下, 发现也是差一点点, 不过这次是第一条不满足.
| A | B | Y |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
与非门 第一项的值是 1, 但 异或门 要求的是 0.
那么, 自然很容易想到, 既然两个都差一点点, 而且差的地方还各不相同, 那能不能把它们先作为一个中间结果, 然后再用一个其它的门组合一下, 看看是否能得到想要的结果呢?
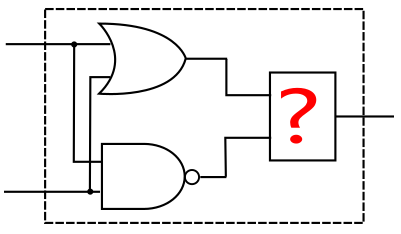
现在, 这个未知的组件显然它应该是 两个输入, 一个输出的, 这样才能套上去. 如此一来, 非门就可以基本排除了.
支持两个输入, 一个输出的门, 盘点一下, 有 与门, 或门, 或非门, 与非门可选, 一一套上去, 然后算出最终的真值表, 就不难发现, 与门 是唯一能满足要求的:
| A | B | X=(A | B) | Y=(A 与非 B) | X & Y | X | Y | X 或非 Y | X 与非 Y |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 |
所以, 最终一个异或门可以通过组合一个 或门 加一个 与非门 再加一个 与门 实现:
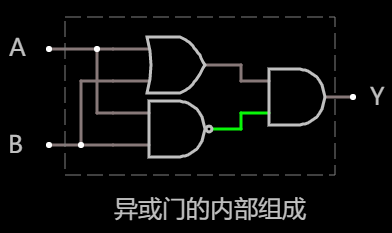
异或门最终实现 在线可互动操作示例
测试一下, 可以看出是符合真值表要求的:
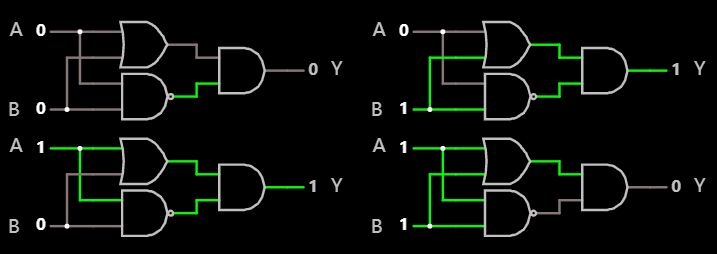
异或门, 四种情况 在线可互动操作示例
通过以上, 我们知道, 哪怕模拟器里没有直接提供 异或门, 也完全可以自行通过其它门搭建出来.
当然了, 这里自行去搭的问题是它还是需要一定的技巧甚至说运气的. 比方说, 你怎么能预料到最后再加个 与门 就能得到想要的结果呢? 或许不行呢? 难道这样一直试凑下去, 但即便一直凑下去, 难道就能保证一定能凑出来吗?
另一个问题则是, 如果凑的组件越多, 级数越多, 推算越来越多层级的真值表也越发的麻烦.
归纳起来, 有两个问题. 一个是 可行性 的问题, 也就是哪怕随便给出一个想要的结果, 是不是一定能够通过组合多个 与门, 或门 以及 非门去实现?
如果没有这种保证, 或许我们就不那么愿意去尝试了, 对吧?
这就有点像 永动机 那样, 如果你知道它是不现实的, 就自然不会去尝试打造它, 因为它造不出来, 所有投入的精力都是白费力气.
第二个问题则是 方法论 的问题, 更准确的说, 是 机械的方法论 的问题, 也就是有没有一套比较机械的方法, 哪怕麻烦一点也行, 只要按部就班去操作, 就能够实现所需的逻辑.
显然, 方法论一定是建立在可行性的基础之上的. 如果没有可行性, 也自然不会有方法论.
而方法论的意义在于, 它不需要你的灵感, 不需要启发, 甚至连观察, 分析乃至试凑都不需要, 哪怕我脑瓜子一点也不灵光, 也能依照步骤去解决问题.
比方说, 一元二次方程的求根公式就是这样的东西, 你拿那些系数去套就完了, 一定能够解出方程的根(或是判断出方程是否有解)
这里不打算去证明它的可行性, 这个已经有人证明过了, 我们关心的主要是方法论. 此外, 有了方法论, 也可以说其实就反过来证明了可行性.
在下一篇章中, 将会来探讨一下这样的方法论.