触发器
在之前, 为了做累加, 需要手动转设锁存器的结果, 这很麻烦, 可否更自动一点呢?
回想到之前学过的反馈的概念, 如果直接把锁存器的输出反馈接回到其中的 A 输入端, 问题似乎就解决了:
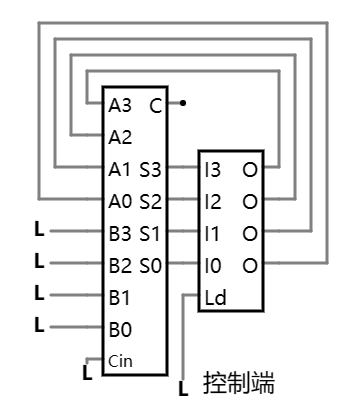
当然, 如此一来只有一个输入端供我们置入加数了, 不过没关系, 可以一次加一个, 三个数就分三次, 比如对计算 1+2+3 来说:
- 首先锁存器的初始值是 0, 反馈到 A 端也是 0;
- 第一次在 B 端置入第一个数 1, 此时 A+B 也就 0+1, 结果是 1;
- 新的结果 1 再反馈回到 A 端, 在 B 端再置入第二个数 2, 此时 A+B 也就 1+2, 结果是 3;
- 新的结果 3 再反馈回到 A 端, 在 B 端再置入第三个数 3, 此时 A+B 也就 3+3, 结果是 6;
听上去似乎 OK, 但实际上呢? 为分析实际可能存在的问题, 我们把电路再简化一下, 暂时先去掉锁存器, 直接把加法器的输出反馈到输入端 A:
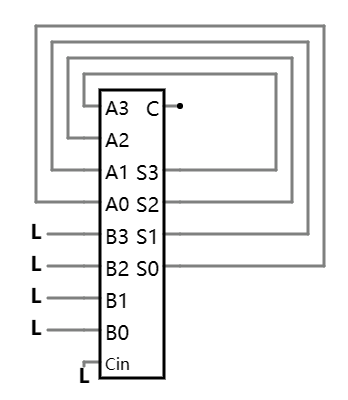
这样一个电路会有什么问题呢? 在初始状态下, 似乎一切也正常. 但这种正常只是一个特例下的假象.
因为目前 B 端输入是 0, 和也是 0, 反馈回 A 也是 0, 0+0=0, 再反馈也依旧是做 0+0=0.
但一旦在 B 端置入一个 1, 那么:
- 0+1=1
- 1 被反馈回 A, B不变还是 1, 于是 1+1=2;
- 2 被再度反馈回 A, 于是 2+1=3;
- ...
经过这个简单分析后我们就不难明白, 仅仅开始置入一个数, 电路本身自己就在不断的运行下去了.
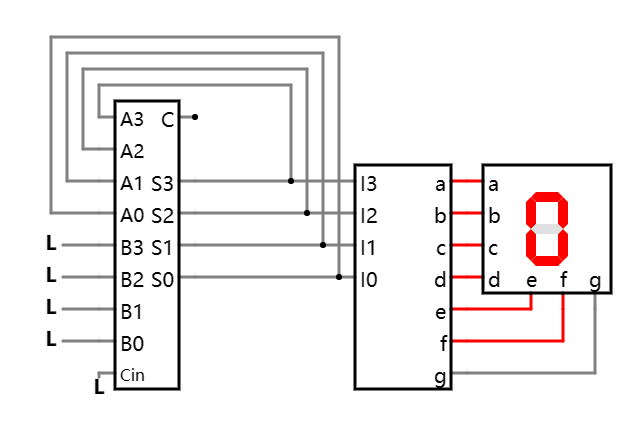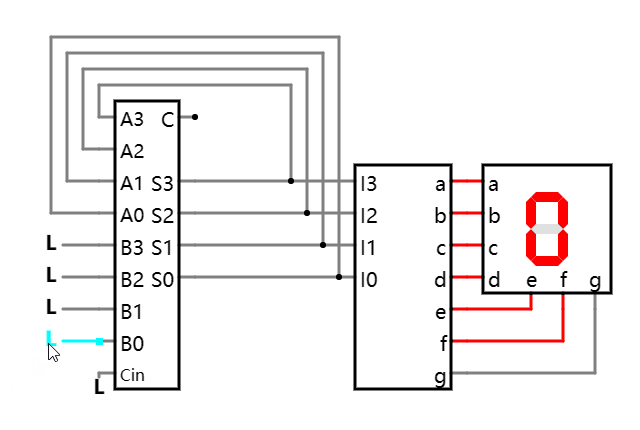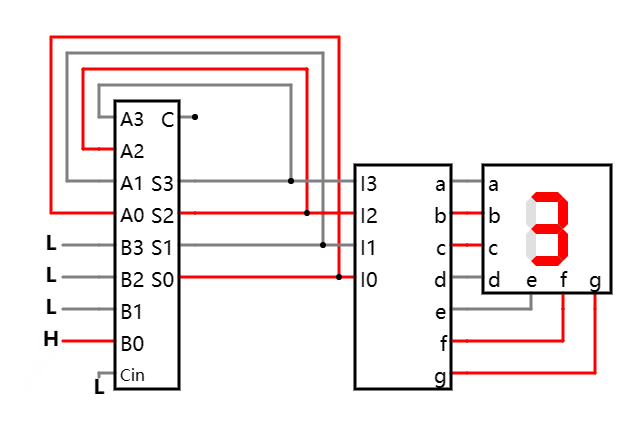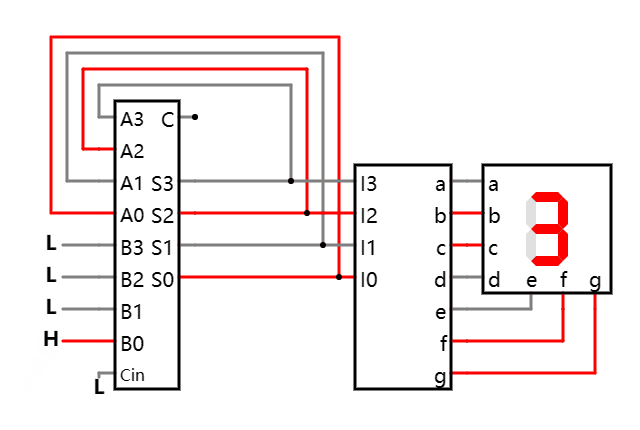
加法器和的反馈循环 在线可互动操作示例
和会一直增加, 直到发生溢出, 回到 0, 然后又继续下一轮的增加, 直至下一次溢出, 如此循环往复不停振荡!
如上: 录制了一个简单 gif 动画.
这里把模拟器的仿真速度设置为一个非常低的值, 并且用了一个七段数码管及相应译码器来显示和的情况.
可以观察到数值并未如我们预期那样变化, 而是呈现 1, 3, 5, 7... 这般变化, 这里涉及到模拟器的具体实现及内部器件的相应速度等一系列因素, 这里就不展开分析了.
不过和会不断变大并重复这一点是确定的.
这倒像是一个简单的 计数器 的原型.
就这个简单的电路而言, 我们根本没机会置入第二个数, 它也无法完成累加的功能.
但你可能想, 我们还有一个锁存器呀, 而且它还有个控制端, 我们是可以手动控制加法器的输出和进入缓存的时机, 从而就控制了和被反馈到 A 端的过程.
事实真的如此吗? 我们仔细分析下. 一开始, 先把锁存器的控制端置为低电平, 然后在 B 端置入第一个加数 1:
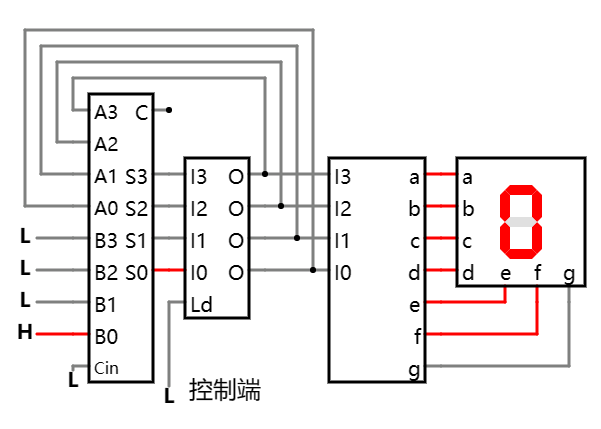
这里为方便观察输出的值, 同样增加了译码器及七段LED数码管.
可以看到, 正如我们期待的那样, 由于锁存器控制端的存在, 加法器的和没有直接穿透锁存器, 因此也并反馈到输入端.
可一旦把控制端设为高电平呢? 仔细一想不难明白, 这时锁存器的屏障作用就不存在了, 本质上跟先前的加法器和输出直接反馈到输入端没有太大区别, 只是多经过一些电路, 多一些延时而已!
所以如果保持锁存器控制端的高电平, 这个电路依然会像先前的电路一般循环! 除非你能及时把控制端再设回低电平.
可你的速度到底要多快呢? 如果设回低电平太快了, 可能加法器的和都还未来得及缓存到! 而如果太慢了, 则电路输出的和就会开始震荡上升!
你得恰到好处的操作, 这可太为难人了!
不过当我们真的把控制端置为高电平时, 和确实被缓存进去了, 但神奇的是, 震荡上升的情况并未发生:
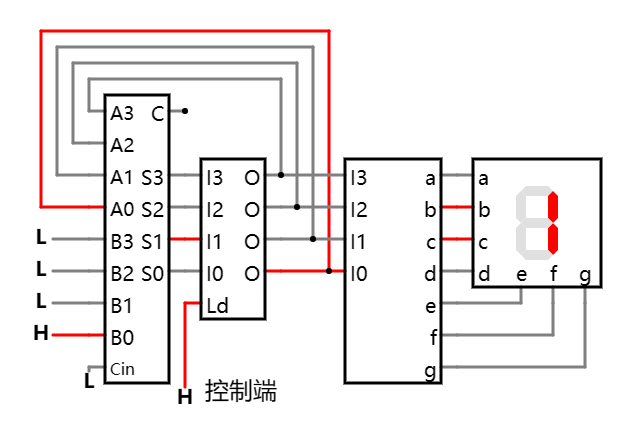
如上, 这并非是我眼疾手快截的图.
当控制端处于高电平时, 先前的和 1 确实被缓存并反馈到了 A 输入端, 然后再次与 B 端原来的 1 相加, 加法器的和可以看到已经变到了 2(0010).
但这个 2 并未穿透锁存器, 而控制端依然是高电平, 为啥电路并未如我们上述分析那般运行呢?
所以为啥开始切换到高电平时, 第一个和能穿透锁存器, 而现在同样是处在高电平, 新的和却仍然被阻隔了呢?
自然, 并非我们的分析出了什么问题, 真正的问题出在系统内置的这个锁存器上.
还记得在先前曾经提到, 这个锁存器的控制端并非是 电平触发 而是 边缘触发 的吗?
更具体的讲, 是上升沿触发. 也即是在电压由低电平变为高电平的那一刻才会触发,
而单纯保持在高电平则不会持续触发, 除非再出现一次由低到高的跳变!
这就是边缘触发与电平触发的不同!
为理解这一点, 可以把控制端的高电平再次复位为低电平, 然后又再度设置为高电平, 这时会发现第二个和 2 就被缓存进去并被反馈到输入端, 而新的输出和则变成了 3.
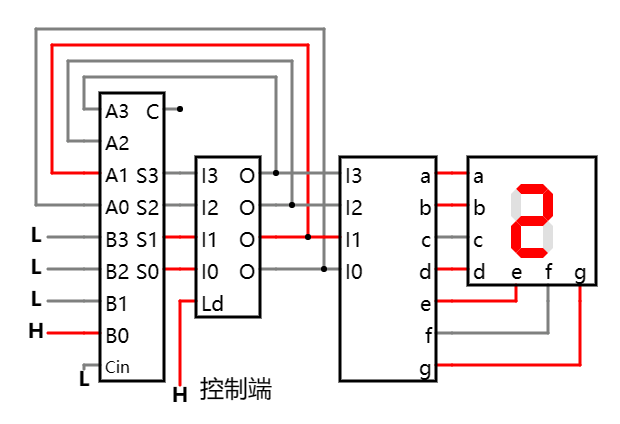
加法器和放触发器的反馈循环 在线可互动操作示例
但这个 3 依然被阻隔了, 为让它穿透, 需要再度把控制端的高电平复位为低电平, 并再次设置为高电平, 反复这样操作就能驱动和不断增加:
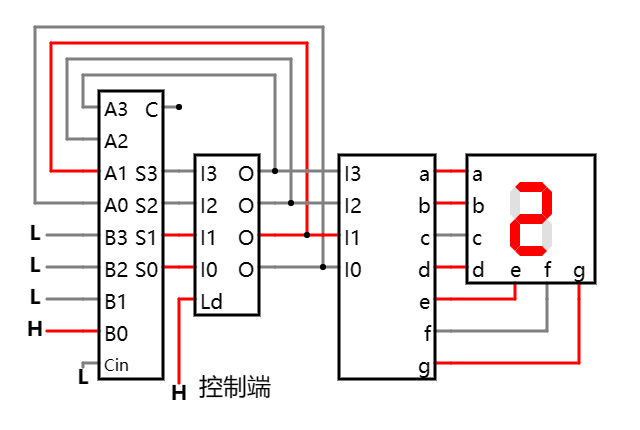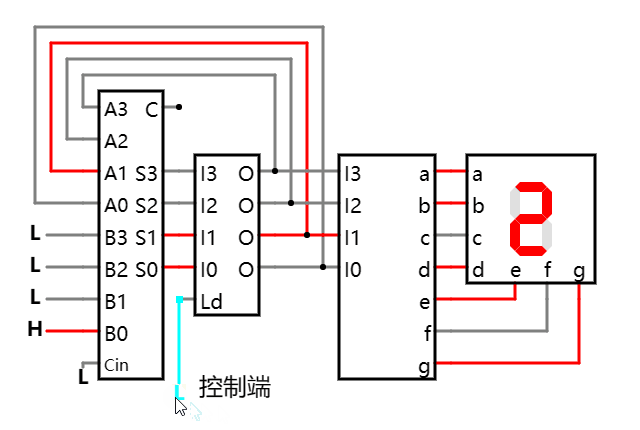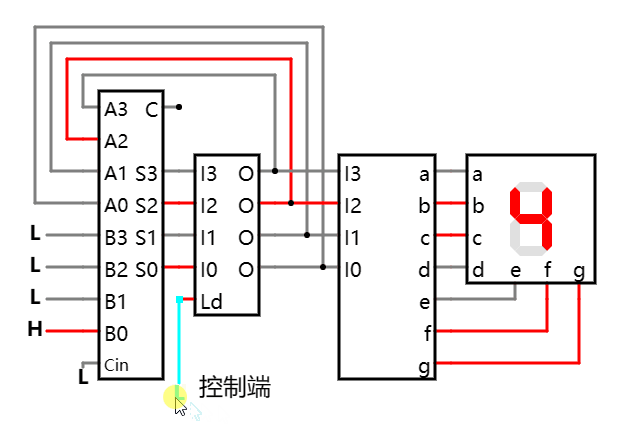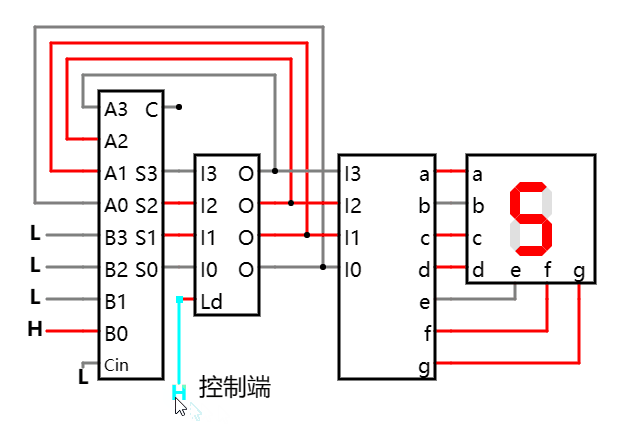
如上: 通过不断点击控制端在高低电平间来回切换, 就能驱动加法器不断作累加.
注: 这里并没有演示 1+2+3 的情况, 当然要做这个也很简单, 只需在下一次切换控制端时, 先把新的加数设置到 B 端即可.
在上面的演示中, 没有改变 B 端加数的值, 始终是第一个值 1, 这里只为演示边缘触发的特性.
在边缘触发的情况下, 可以从容地控制每一个步骤. 对于边缘触发的控制端, 更合理的选择是使用之前曾经提到的 "按钮开关", 也就是与我们手机电脑电源开关类似的那种, 按下后松手它会自动松开.
从这点上看, 电脑的开机大概率是一个边缘触发驱动的.
每按一次, 就触发一次保存; 另一方面, 即便是按住不放, 一直处在高电平也不会持续触发, 这就解决了电平触发所带来的问题, 无需精确地把握时机, 动作也不需要特别快.
所有这些都是边缘触发带来的好处. 之前曾提到, 在此书中, 我们约定把边缘触发的存储器称为触发器(Flip-Flop), 而由电平触发的存储器则默认为锁存器(Latch)
但在其它很多地方, 则可能没有这么明确的区分, 包括 circuitjs 系统里, 它所提供的锁存器实质上是边缘触发的.
当使用作存储时, 区分得通常没那么清晰, 当然触发器的用途不仅仅是存储, 这里只是从存储的角度引入了触发器的概念.
它只在电平跳变边缘触发的特性恰好解决了我们面临的问题. 在之前的传输门里, 我们已经理解了电平触发的原理, 那边缘触发这种神奇特性是如何实现的呢? 我们将在后续的篇章中加以分析.