分而治之法实现 2 的显示
除整体考虑法之外, 另一种方式是应用前面多次提到的 分而治之(Divide and Conquer) 的原则. 如果说七个段的情况有点太复杂了, 一下子没有思路的话, 则完全可以按照之前处理半加器时分成 进位器 和 加位器 两个模块的思路去处理.
只不过你现在有七个模块而已, 每个模块分别负责 a, b, c, d, e, f, g 的最终状态, 所有模块的输入都是 C 和 S, 也即是半加器的输出:
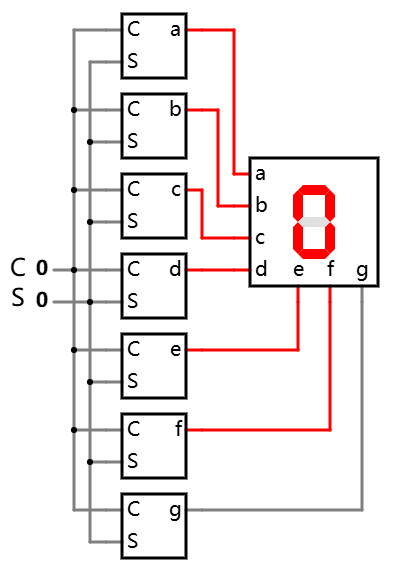
LED 解码, 分七个模块 在线可互动操作示例
数量虽多, 但单个来看, 都是简单的 两输入单输出 的模块. 如此一来, 一个看上去比较复杂的大问题, 就变成了多个独立的简单的小问题.
结合前面谈到的 自定义逻辑 方式, 你可以添加 7 个不同的自定义逻辑即可.
当然, 这里不是真的要再次用自定义逻辑去实现. 但你会发现, 用 自定义逻辑 的方式先去界定 输入与输出 是一种很方便的方式, 通常, 这被称为确定 接口(interface).
分析
根据 0, 1, 2 各自需要点亮的段列一个表:
| 数字 | a | b | c | d | e | f | g |
|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 2 | 1 | 1 | 0 | 1 | 1 | 0 | 1 |
清点一下三种情况, 首先 b 都是要亮的(三种情况都是 1), 所以 b 直接连电源即可;
而 a, d 和 e 的模式是一样的(都是 101), 因此只需要一个 a 模块, 其它两个复用 a 的输出即可, 最终简化为:
| 数字 | a | c | f | g |
|---|---|---|---|---|
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| 2 | 1 | 0 | 0 | 1 |
如此下来, 不用整七个, 只要设计四个模块即可.
把半加器输出端 C, S 作为数码管的输入端, 四种输出需要对应的结果如下:
| C | S | a | c | f | g |
|---|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 1 |
初步观察一下, 就不难发现, g 与 C 是完全一样的(都是 001), 因此所谓的 g 模块既不需要两个输入, 甚至连唯一的一个输入 C 都不需要再进任何处理, 直接用导线把 C 和 g 连起来即可.
| C | g |
|---|---|
| 0 | 0 |
| 0 | 0 |
| 1 | 1 |
因为 g 就是中间那段, 只是在显示 2 时才需要点亮, 显示 0 和 1 时恰好都不用点亮.
而另一方面, C 恰好是进位输出, 表示结果至少是 2, 不会是 0 和 1, 所以正好可以以此作为区分.
当然, 这里能够如此简化, 是因为目前只考虑了 0, 1, 2 三种情况, 如果要显示更多的数字, 恐怕就没法如此简单处理了.
但就目前的情况而言, 这样做是 OK 的.
再进一步观察, 又可以发现, 单独对 S 取反即可得到 a:
| S | !S | a |
|---|---|---|
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
然后, 单独对 C 取反即可得到小 c:
| C | !C | c |
|---|---|---|
| 0 | 1 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
f 模块的处理
最后, 仅需要处理 f 段的情况:
| C | S | f |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
f 怎么去实现呢? 有时如果你看不出什么规律, 不妨先把它补充为四种情况的模式, 而四种情况的模式我们已经知道的有 串联模式, 并联模式, 加位器模式.
f 模块, 方式一
现在, 因为 C 和 S 均为 1 的情况我们可以忽视, f 在此种情况下可以为 0 也可以为 1, 假如为 0:
| C | S | f |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
显然, 它不符合上述所列的串联, 并联以及加位器模式中的任何一种, 但简单把 f 取个反(用 !f 表示):
| C | S | f | !f |
|---|---|---|---|
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 |
!f 与两个输入 C 和 S 的关系, 这不就是 并联模式(Parallel) 吗?
| A | B | P |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
所以你只需将 C 和 S 并联, 最后再用继电器做一个反向即可.
当然, 如果你对几种模式及取反的情况比较熟悉, 你不需要补充第四种组合也很容易看出使用并联再取反即可满足要求.
f 模块, 方式二
同理, 假如 f 最后的值为 1, 结果是:
| C | S | f |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
显然, 它也不符合我们已知的所有模式, 但同样简单把 f 取个反(用 !f 表示):
| C | S | f | !f |
|---|---|---|---|
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
!f 与两个输入 C 和 S 的关系, 这不还是 加位器模式 吗? 就是那个天平模式, 也就是那个跷跷板电路:
| A | B | S |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
所以你只需将 C 和 S 再用一个加位器的电路组合起来, 最后再用继电器做一个反向同样可行.
最终, f 模块可以有多个实现方式, 你可以根据自己需要选用.
综合
一个使用并联模式并取反的方案最终如下:
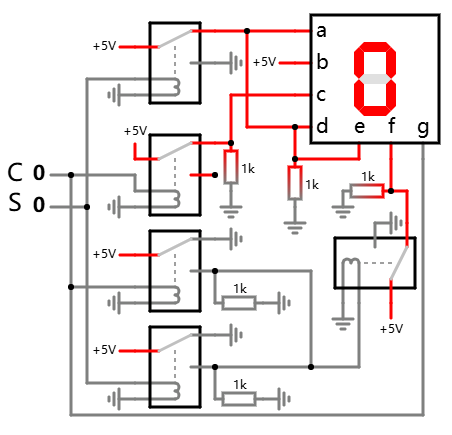
LED 解码采用分解法的一种最终实现 在线可互动操作示例
整体看上去可能稍显凌乱, 但每个段一一单独去看, 其实都很简单.
要么直连电源, 要么直连某个输出, 要么对某个输出简单取反;
最复杂的也不过就是 f 模块: 先对两输出并联, 再对并联的结果取反.
此外, 在继电器处添加的电阻和接地是为解决前面提到的电压悬空问题.
上图中显示了 0 的情况, 经测试, 显示 1 和 2 两种情况均可以满足:
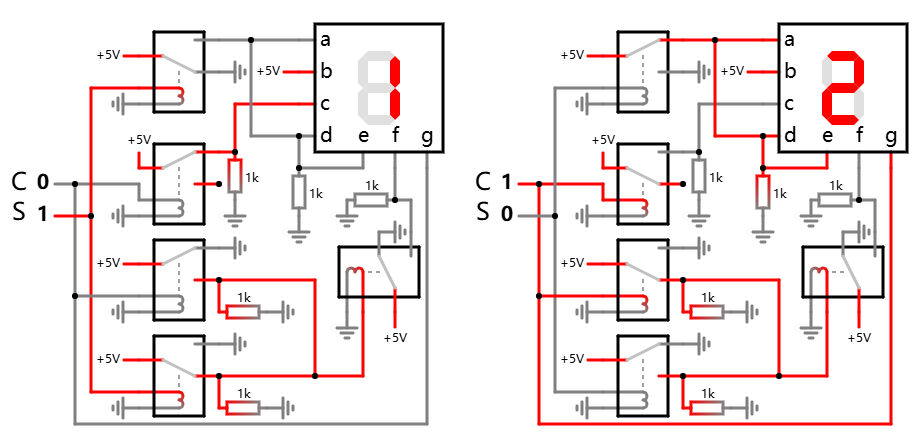
如果你还是不太明白它为何可行, 最简单的方式就是一一跟踪那些导线的高亮状态, 为什么这根线是绿的, 为什么那根是灰的, 是怎么导致的.
搞清楚它们为何处于这样的状态就不难明白整个的原理了.
综上, 虽然问题在一开始看起来比较麻烦, 但经过分解及仔细分析, 问题被简化并得到一一解决, 最终的解码电路也不算特别复杂.
当然, 这与我们仅仅显示 0, 1, 2 三种情况也有关.
小结
现在, 来小结一下整个过程. 可以看到, 分而治之还是一个挺有用的策略. 它能够让一个大问题变成很多个小问题.
而一旦问题变小, 寻求解决方案就简单很多了. 而且在这个过程中, 你会发现一些相似的问题, 一些简单处理即可解决的问题. 最后你也许只剩一两个稍难的问题.
如果你在工作, 假如这是上级分配给你的一个任务, 你把它分解了, 然后把很多简单模块都解决了, 只剩较难一点的 f 模块. 当上级询问起你进度的时候, 你可以说:
七段已经通了六段, 就(还剩)一段不通了.
一般来说, 你的上级不会太细究里面的细节, 你是不是剩下了最难的一段, 他一般不关心的. 他只会很高兴地觉得进度已经完成了 6/7, 你干得不错!
当然, 也许你会碰到比较苛刻一点的领导, 他会仔细检查你的工作, 然后发现最难的一段你还没有实现, 他可能会向你抱怨:
什么叫只剩一段不通了? 这是最关键的好不好? 什么七段通了六段, 我看你是"七窍通了六窍 -- 一窍不通!"
如果真是摊上这样的领导, 只能说有点运气不好了! 不过严格来讲, 你说七段已经通了六段, 你并没有撒谎呀! 仍然是实事求是的嘛!
其实, 如果你善于分解你的任务, 哪怕最后剩一些你完成不了子任务, 你也可以请求领导将其分配给其它团队成员去协助完成. 任务分得好, 这种团队协助才有可能, 也才能更高效.
天大的任务, 就拿秦始皇统一天下来说吧, 不也是分而治之, 各个击破吗?
展望
最后, 你可能还会有些困惑及担心, 现在的电路都比较简单, 因此通过简单的观察, 分析就基本能够找到解决方案.
但如果问题越来越复杂呢? 比如如果还要同时显示更多的数字, 比如 3, 4, 5 直到 9 等等, 另一方面, 也同时需要更多根输出线的参与, 不再是两线, 而是三线甚至四线的情况, 还靠这种观察找规律的方式恐怕是不行的.
你可能要问, 有没有更加正规一些的方式, 比如就像解一元二次方程的求根公式那样的, 只需要套公式, 然后按部就班的操作就能设计出我们想要的电路呢?
嗯, 这样的方式确实是有的, 但需要在后面再去介绍, 我们还需要其它一些基础的准备, 另外可以看到, 即便是仅仅解码 0, 1, 2 的显示, 需要的电路器件及相关连线还是不少的.
因为目前我们只知道继电器这样的方式去实现, 但它相对来说还是比较麻烦, 接下来会讲一讲晶体管以及门电路方面的知识, 这可以为以后设计越发复杂的电路打下一个良好的基础.